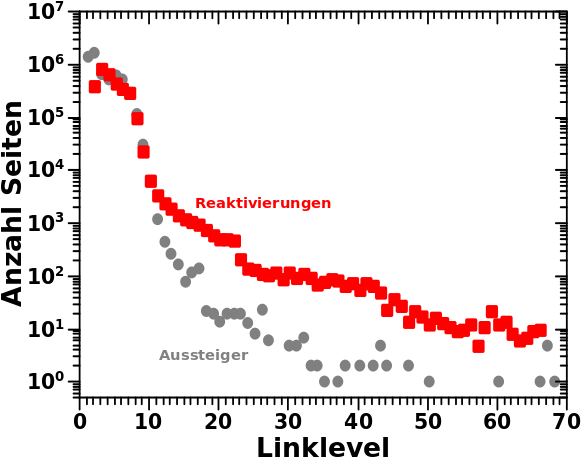
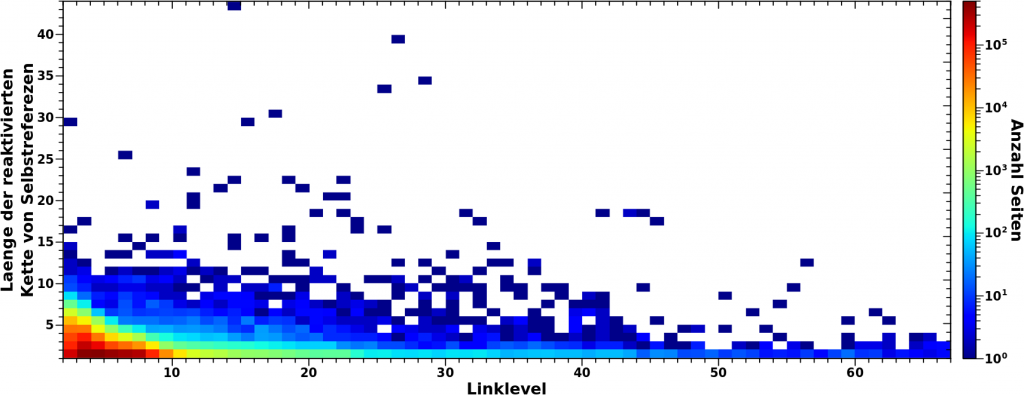
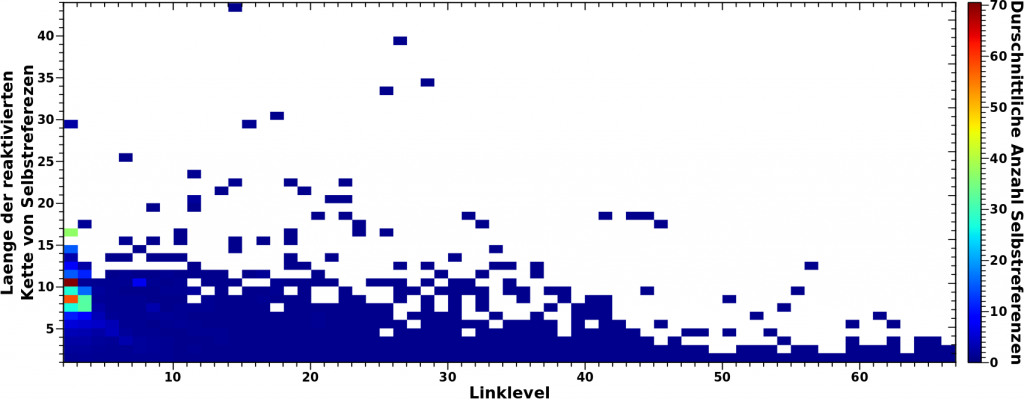
Zum Ende des letzten Beitrags zeigte ich (an drei Beispielen), fuer wieviele Seiten die Kette an Selbstreferenzen abbricht. Dies in Abhaengigkeit vom Linklevel und von der Anzahl der Selbstreferenzen. Ich erwaehnte auch, dass man diese Information nutzen kann um die Diskrepanzen zwischen Simulation und Messung (auf Seiten der Simulation) zu reduzieren (oder zumindest zu erklaeren).
Wie ebenso beim letzten Mal erwaehnt, so muesste man, um das ordentlich zu machen, den (mehr oder weniger) allgemeingueltigen Zusammenhang zwischen Anzahl der „Aussteiger“, Linklevel und Anzahl der Selbstreferenzen in Form einer Funktion ermitteln … was mir zu viel Arbeit ist. Da ich nur mal schauen will, wie gut diese einfache Korrektur funktioniert, werde ich hier einen hybriden Ansatz verfolgen, bei der ich Simulationsresultate und Beobachtungen „vermischen“ werde. Fuer eine richtige Simulation kann man das natuerlich nicht so machen.
Das Ganze werde ich auch nicht allgemein machen sondern an einem sehr konkreten Beispiel: die Diskrepanz zwischen Simulation und Messung auf LL7 fuer Seiten die auf LL7 10 Selbstreferenzen haben. Ihr meine lieben Leserinnen und Leser seid sicher schlau genug das verallgemeinernte Prinzip dahinter zu erkennen.
Zur Erinnerung nochmals der Vergleich zwischen Simulation und Messung (linkes Diagramm) und auszerdem die Anzahl der Aussteiger in Abhaengigkeit von der Anzahl der Selbstreferenzen fuer LL4 bis LL6.
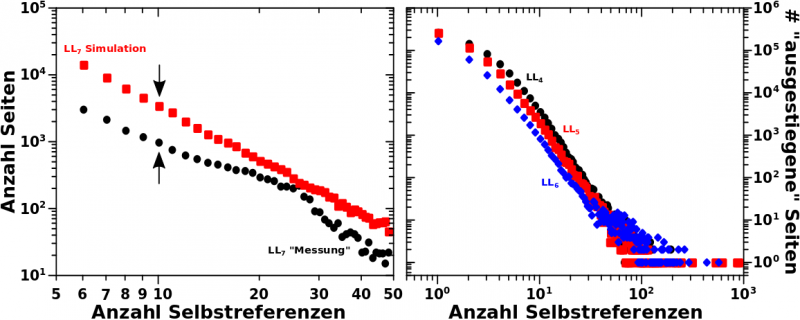
Los geht’s mit der simplen Beobachtung, dass die simulierte Anzahl Seiten auf LL7 mit 10 Selbstreferenzen gleich 3428 ist waehrend der „gemessene“ Wert nur 967 betraegt. Das ist eine Diskrepanz von 2461.
Der simulierte Wert ergibt sich aus der simulierten Entwicklung des Systems, welche mit diesem maechtigen Gesetz beschrieben wurde:
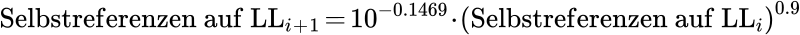
Von hier aus muessen wir rueckwaerts rechnen um heraus zu finden, welche Seiten auf LL6 zu Seiten mit 10 Selbstreferenzen auf LL7 gefuehrt haben. Wenn man das tut erfaehrt man, dass auf LL6 Seiten mit 17, 18, 19 und 20 Selbstreferenzen anteilsmaeszig zu Seiten mit 10 Selbstreferenzen auf LL7 gefuehrt haben.
Wie bitte? Wie kønnen denn 4 verschiedenartige Seiten zu nur einem Wert fuehren? Die Antwort darin, dass die Anzahl an Selbstreferenzen nur ganzzahlig sein kann und erklaert warum das Wørt „anteilszmaeszig“ im obigen Satz wichtig ist. Ein Beispiel macht das Ganze etwas anschaulicher.
Eine Seite mit 17 Selbstreferenzen auf LL6 hat nach dieser Formel 9.129 Selbstreferenzen auf LL7. Kønnte man ja erstmal denken, dass das leicht auf 9 abzurunden ist. Aber wie beim letzten Mal explizit erwaehnt, wird mit der Entwicklungsgleichung nur der Durchschnitt der Selbstreferenzen auf dem naechsten Linklevel berechnet. Nun habe ich aber mehr als eine Seite mit 17 Selbstreferenzen auf LL6 und wenn ich das Ergebniss fuer alle auf 9 abrunde, dann stimmt das nicht mehr mit der Formel ueberein.
Deswegen habe ich mich entschieden, dass (fuer diesen Fall, was aber repraesentativ ist fuer den allgemeinen Fall) 12.9 % (also der Anteil nach dem Komma) aller Seiten mit 17 Selbstreferenzen auf LL6 zehn Selbstreferenzen (also eine mehr) auf LL7 haben wird. Damit stimmt der Durchschnitt wieder.
Von den Seiten mit 18, 19 bzw. 20 Selbstreferenzen auf LL6 tragen jeweils 61.0 %, 91.0 % bzw. 43 % zu Seiten mit zehn Selbstreferenzen auf LL7 bei.
Das war die erste Sache. Nun muessen wir im rechten Diagramm nachschauen, wie viel Seiten mit 17 (bzw. 18, 19 oder 20) Selbstreferenzen auf LL6 es in Echt niemals bis LL7 schaffen (die ich aber in der Simulation „mitschleife“). Das sind 130 (bzw. 100, 104 und 76) Seiten. Davon darf ich fuer den ganz konkreten Fall hier natuerlich nur den Anteil beruecksichtigen, der dem obigen Anteil entspricht. Das heiszt ich kann vom simulierten Wert von 3428 Selbstreferenzen nur 205 (= 17 + 61 + 94 + 33) Seiten abziehen.
Zwischenbemerkung: den Wert kann man einfach abziehen, denn die Anzahl der Aussteiger muss NICHT korrigiert werden bezueglich der Aussteiger auf frueheren Linkleveln. Das liegt daran, weil die „experimentellen“ Daten bzgl. der Aussteiger pro Linklevel natuerlich _nur_ anhand der „Ueberlebenden“ ermittelt wurden. In der Messung werden schlieszlich keine Seiten „mitgezogen“ die da nicht sein sollten.
Auch wenn es hier nichts ausmacht, so ist es wichtig solche Sachen zu diskutieren, denn da kann man u.U. schnell in eine „Falle“ tappen.
Das war aber nur der erste (Rueckwaerts)Schritt und muss fuer den Uebergang von LL6 zu LL5 und dann nochmal von LL5 zu LL4 wiederholt werden. Dabei erweitert sich der Bereich der beitragenden Seiten zunaechst auf alle Seiten mit 32 bis 42 Selbstreferenzen auf LL5 und dann noch mehr auf alle Seiten mit 67 bis 95 Selbstreferenzen auf LL4.
Die Summe der aussteigenden Seiten betraegt 199 auf LL5 und 82 auf LL4. Die letzte Zahl wird trotz des erweiterten Bereichs beitragender Seiten kleiner, weil die Anzahl der aussteigenden Seiten mit wachsender Anzahl an Selbstreferenzen so schnell abnimmt. Das ist auch der Grund, warum in (!) diesem Fall der Schritt zu LL3 (dem Ausgangszustand) nicht gemacht werden muss, denn das faellt nicht mehr signifikant ins Gewicht. Aber Vorsicht! Betrachtet man Seiten mit deutlich weniger als 10 Selbstreferenzen auf LL7 so gilt das im Allgemeinen nicht!
Summa summarum verringert sich durch diese Korrektur die Diskrepanz zwischen gemessenen und simulierten Werten auf 1975.
1975 hørt sich erstmal immer noch voll viel an, aber das entspricht ca. 20 % des unkorrigierten Wertes. Das ist aber eigentlich ziemlich gut, denn eine „Erklaerungskraft“ von 20 % mit einer solch einfachen Erklaerung ist im Allgemeinen nicht zu erwarten. Das miss inbesondere mit Hinblick auf die Einfachheit des Modells gesehen werden und dass wir wissen, dass die Entwicklungsparameter eigentlich NICHT konstant sind, dadurch ein groszer „Fehlerbeitrag“ von Anfang an zu erwarten ist.
Dies alles ist uebrigens warum ich beim letzten Mal schrieb:
[d]as waere sogar eine Korrektur mit „langfristiger“ Wirkung.
Aber was ist nun mit den restlichen 80 % Diskrepanz? Eine weitere relativ simple Korrektur ist der Grund warum ich (auch) beim letzten Mal sagte:
Der ziemlich grosze Unterschied […] zwischen Median und Mittelwert wird beim naechsten Beitrag nochmal wichtig.
Ich merke nun, dass ich damit stark uebertrieb, denn ich werde das hier nicht im Detail erlaeutern. Aber kurz gesagt wuerde ich vermuten, dass der Gebrauch des Medians anstelle des Mittelwerts zur Ermittlung der Entwicklungsparameter, zu (in der Summe) weniger Selbstreferenzen im jeweils naechsten Schritt fuehren wuerde. Eine solche Korrektur wird vermutlich einen weiteren nicht zu vernachlaessigenden Beitrag leisten. Mein Bauchgefuehl sagt mir so nochmal 20 %
Noch besser waere natuerlich, wenn man eine Verteilung um den Mittelwert (oder Median) nehmen wuerde. Beide Sachen sind leicht einzusehen, aber ich habe keine Lust mehr das alles nochmal zu machen.
Aber selbst damit wuerde ich nur ca. 50 % der Diskrepanz erklaeren kønnen. Der Rest ist halt so und liegt (wieder) an der Einfachheit des Modells und dass die Entwicklungsparameter in Wirklichkeit nicht konstant sind.
Puuh … genug fuer heute und im Wesentlichen genug zur Simulation an sich. Ich denke, dass die Selbige hinreichend erfolgreich war … hab ja auch genuegend Zeit damit verbracht.
Beim naechsten Mal werde ich die Simulation zwar nochmal kurz erwaehnen aber nur als Ueberleitung um mir mal anzuschauen wie es aussieht, wenn ausgestiegene Seiten nochmal „zurueck kommen“.