Zur Erinnerung: hier zog ich als Analogon zu den Selbstreferenzen die Geschwindigkeitsverteilung von Gasteilchen in einer heiszen Box heran … und diskutierte dort inwieweit das zulaessig bzw. auch vøllig unzulaessig ist. Dieses Analogon werde ich auch heute benutzen.
Bei einer Simulation bzgl. der Entwicklung eines Systems braucht man zunaechst einen Anfangszustand. Der Anfangszustand bzgl. der Selbstreferenzen ist natuerlich LL0 … aber da gibt es keine Selbstreferenzen (von Artefakten abgesehen) und das entspricht einem klassischen (definitiv nicht quantenmechanischem!) Gas mit einer absoluten Temperatur von 0 K. Null Kelvin ist schwerlich als heisz zu bezeichnen … tihihi.
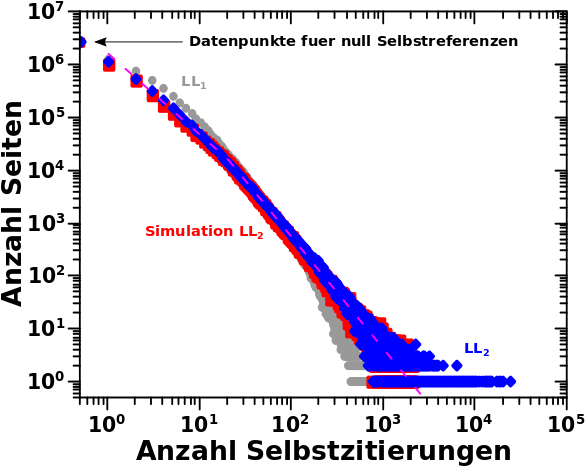
Wie sieht’s denn mit LL1 als Ausgangszustand aus? Das ist zwar besser, aber wir wissen, dass es sich bei der Verteilung auch um eine Ausnahme handelt, ist diese doch selbst mit Augen zudruecken nicht linear (bei doppellogarithmischer Darstellung). Im Analogon kønnte man sich vorstellen, dass bei LL1 die Heizplatte noch angestellt ist und definitiv noch kein Equilibrium im Gas erreicht wurde. Gleichgewicht mit dem „Aeuszeren“ sowieso nicht, denn das ist ja der Entwickluingsprozess (am Gasbild: das Abkuehlen) den ich simulieren will.
Dann also LL2 … jup … das geht gut genug linear, im Bild des heiszen Gases ist die Heizplatte also ausgeschaltet. Aber … mhmmmm … da ist ein kleiner Knick in der Kurve … ach dann beschreibe ich das abschnittsweise linear, eine Funktion fuer Werte zwischen 2 und 20 und eine andere fuer alles darueber … da kønnte man sich denken, dass die Heizplatte noch ein ganz klein bisschen Restwaerme hatte und der Knick durch die paar wenigen Gasteilchen zustande kommt die sich nochmal schnell „aufgewaermt“ (also Energie erhalten) haben und die daraus resultierende høhere Geschwindigkeit noch nicht durch Støsze mit den restlichen Teilchen abgegeben haben. Aber wie gesagt ist der Vergleich von Gasteilchengeschwindigkeiten und Selbstreferenzen physikalisch (und mathematisch) gesehen vølliger Quatsch. Aber ein Analogon dient ja zur Illustration eines weniger leicht fassbaren Sachverhalts mit einer bekannten Sache. Und all das hier schreibe ich um zu illustrieren, dass es auch in anderen Systemen Sachen gibt die nicht in das ideale Bild passen, man dafuer aber immer Gruende finden kann.
Wenn man das so mit den Regressionsgeraden macht, dann liegen mir die Werte fuer keine und eine Selbstreferenz(en) etwas weit abseits der ersten Geraden. Da nehme ich dann lieber die experimentell ermittelten Werte bzgl. dessen wie wahrscheinlich das ist, keine oder eine Selbstreferenz(en) zu haben. Zum Zweiten sind die Verteilungen auf LL2 und LL3 ja beinahe deckungsgleich. Deswegen wird LL3 fuer die Simulation der Entwicklung des Systems als Ausgangszustand angesehen.
Wieauchimmer, wenn man das alles so macht und dann die Anzahl der Selbstreferenzen 6 Millionen mal simuliert (jedes „Gasteilchen“ muss separat simuliert werden), dann ist der simulierte Ausgangszustand eine (fuer die hiesigen Zwecke) hinreichend gute Naeherung. Dies und (fast) alles was ich Oben schrieb ist in diesem Diagramm nochmals zu sehen:
Eine Sache faellt auf: der lange „Schwanz“ der blauen Verteilung wird nicht durch die (zweite oder erste) Regressionslinie beschrieben. Das kann man fixen, ich habe das aber der Einfachheit halber nicht gemacht. Deswegen der „Abbruch“ in den roten Punkten bei 3000 Selbstreferenzen … mal schauen, wie sich das im weiteren Verhaelt.
So, das war’s … … … aber ich møchte an dieser Stelle ein bisschen darauf eingehen, wie ich von der gemessenen Verteilung der Selbstreferenzen auf LL1 zur Simulation derselbigen komme (abgesehen von dem bereits Gesagten).
Zunaechst einemal gilt natuerlich, dass diese Verteilung eine Wahrscheinlichkeitsverteilung ist … wenn man diese durch die Anzahl aller Seiten dividiert. Beim IQ ist das mit einer Normalverteilung leichter vorstellbar (Letzteres gilt auch fuer die Maxwell-Boltzmann-Verteilung der Geschwindigkeit von Gasteilchen). Aber die zugrundeliegende Mathematik ist die gleiche: wenn ich zufaellig eine Seite (Teilchen) aus dem Ensemble heraus nehme, so hat diese(s) eine bestimmte Wahrscheinlichkeit eine bestimmte Menge an Selbstreferenzen (Geschwindigkeit) zu haben. Die mathematische Funktion p in Abhaengigkeit von der Anzahl der Selbstreferenzen x der hiesigen Wahrscheinlichkeitsverteilung sieht so aus:
Wie oben geschrieben: explizit definierte Wahrschienlichkeiten fuer keine und eine Selbstreferenz(en) und zwei (bei doppellogarithmischer Darstellung lineare) Funktionen darueber hinaus.
Soweit ist das noch ganz einfach. Nun kommt aber der Haken an der Sache. Fuer eine zu simulierende Seite muss ich die Anzahl der Selbstreferenzen, also das x (!), berechen, habe aber nur p(x). Letzteres ist im Einzelfall nur sinnvoll wenn man x schon hat, aber die Gesamtheit aller Einzelfaelle muss p(x) ergeben. Aber wenn ich die erste Seite simuliere dann weisz ich ja noch nicht, wieviele Selbstreferenzen alle anderen Seiten haben.
Ich gebe zu, dass ich beschaemend lange brauchte um auf die Løsung zu kommen, aber letztlich ist’s ganz einfach. Doch dafuer muss ich ein bisschen ausholen.
Wenn ich eine Seite simuliere (und ich mache das 6 Millionen mal), dann ziehe ich eine zufaellige Zahl zwischen Null und Eins. Die Abschnitte auf dieser Zahlengerade von Null bis Eins entsprechen dann der Summe der Wahrscheinlichkeiten bis zu einer gegebener Anzahl an Selbstreferenzen. Also 0 bis 0.4561 wird null Selbstreferenzen zugeordnet, 0.4561 bis 0.6458 (= 0.4561 + 0.1897) einer Selbstreferenz und danch muss das entsprechend berechnet werden und die Abschnitte werden sehr schnell sehr klein.
Mathematisch ausgedrueckt entspricht diese zufaellige Zahl dem bestimmten (!) Integral unter obiger Kurve von Null bis zu einer gegebenen Anzahl an Selbstreferenzen. Anders als sonst ueblich bin ich also nicht an dem Wert des Integrals interessiert (denn das ist der Wert aus der zufaelligen Ziehung und somit bekannt), sondern am oberen Limit.
Fuer null und eins kann man sich einfach den Zufallswert anschauen und das sofort rausbekommen. Fuer alle anderen muss das berechnet werden und dabei ist zu beachten dass das Integral dann natuerlich erst bei der richtigen unteren Grenze (also 1 oder 20) los geht (um die vorhergehende Bemerkung einzubeziehen).
Ist das schøn, dass wir es so oft mit maechtigen Gesetzen zu tun haben! *froi*. Da ist das Integral einfach zu berechnen und leicht nach x umzustellen und somit kann jedem gezogenen Zufallswert eine Selbstreferenz zugeordnet werden.
Dabei sind zwei Sachen zu beachten. Zum ersten muss der Zufallswert korrigiert werden. Der Grund liegt in dem was ich oben schrieb: dieser Wert ist die SUMME aller Wahrscheinlichkeiten (bis zu der dem Zufallswert zuzuordnenden Anzahl an Selbstreferenzen). Das (bestimmte) Integral geht aber erst bei den gegebenen Grenzen los, faengt also bei Null zu „zaehlen“ an. Das ist aber ganz einfach, denn vom besagten Zufallswert muss nur die Summe der Wahrscheinlichkeiten bis zu dem Wert ab der die jeweilige Funktion gueltig ist (also bis 1 bzw. bis 20) abgezogen werden.
Zum Zweiten kommen da natuerlich krumme Zahlen raus und die muessen auf die naechste ganze Zahl gerundet werden. Werte die kleiner als 1.5 sind werden zu eins abgerundet. Das ist aber doof, denn Seiten die nur eine Selbstreferenz haben sind ja durch die Fallunterscheidung alle schon erledigt. Der Einfachheit halber habe ich solche simulierten Seiten dann nur rausgeschmissen. Dadurch fehlen ca. eine halbe Million Seiten … das kann man sicherlich fixen, ich hatte aber keine Lust mehr und schmeisz das einfach in den beruehmten „ca.-10-Prozen-Fehler“.
Mit dem letzten und diesem Mal kommen da ein paar krasse Vereinfachungen zusammen. Beim naechsten Mal zeige ich, wie weit man damit dennoch kommt.
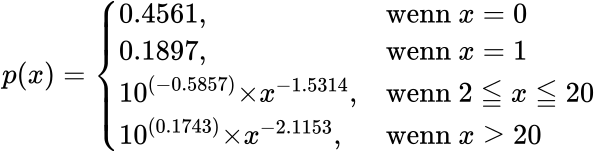
Leave a Reply