Søren in Norwegen

Bereits frueh stiesz ich auf das damals so benannte „São-Paulo-FC-Artefakt“ und es begegnete mir innerhalb des Kevin Bacon Projekts immer und immer wieder. Artefakt deswegen, weil ich zunaechst dachte, dass es durch die Behandlung der Daten vor der eigentlichen Linknetzwerkanalyse zustande kam. Weitere Untersuchungen zeigten aber, dass das gar kein Artefakt ist, sondern ein Phaenomen innerhalb der Wikipedia welches sich allgemeiner beschreiben laeszt.

Zur Auffrischung und ganz kurz, handelt es sich dabei um thematisch zusammenhaengende Seiten die (mehr oder minder, aber oft buchstaeblich) chronologisch sortiert sind und bei der eine Kettenseite jeweils nur die direkt nachfolgende (oder vorhergehende, aber das ist nicht zwingend) zitiert. Das bedeutet, dass bei der Linknetzwerkanalyse alle anderen (nicht zur Kette gehørenden) Seiten ein Kettenglied nach dem anderen „durchschreiten“ muessen. Dies wiederum erklaert andere Beobachtungen. Insbesondere den langen „Schwanz“ in den gemessenen Grøszen, obwohl die allerallerallerallermeisten Seiten bereits nach weniger als 10 Linkleveln den allerallerallerallergrøszten Teil ihres Linknetzwerks gesehen haben.

Ich setzte mich dann daran solche Kettenseiten systematisch zu finden und das hab ich im Zuge der Reproduktion natuerlich nochmal neu gemacht.

Das Wichtigste zuerst: in den neueren Daten (von Ende 2023) gibt es das „São-Paulo-FC-Artefakt“ noch … da freue ich mich, denn es ist mir irgendwie ans Herz gewachsen. Es ist aber nicht mehr die laengste Kette sondern nur noch die viertlaengste und bereits auf LL₃₅ hørt man das letzte Mal von ihr. Das ist natuerlich keine Kuerzung der Kette an sich ist, sondern kommt sicherlich durch eine bessere Verlinkung der Seiten zustande.

Der neue Kettenkønig sind die Tage des Meshir (ein Beispiel) … Huh? 30 Tage sind doch gar nicht lang genug. Wie kann das bis LL₇₈ durchhalten? Die Erklaerung liegt darin, dass dies nur eine Teilkette ist, die rueckwaerts gehend mit den Tagen des Tobi (ein Beispiel) und dann des Koiak (ein Beispiel), und irgendwie vorwarts gehend aber mlgw. parallel (?) mit den Tagen des Paremhat (ein Beispiel) eine zusammenhaengende Kette bildet. Wobei die Verlinkungen sicherlich komplizierter sind als beim „São-Paulo-FC-Artefakt“ (welches der Tradition wegen weiterhin von mir als „Artefakt“ bezeichnet wird). Letzteres endet naemlich wie erwartet in 1930, …

[…] the first competitive season of São Paulo Futebol Clube […]

… waehrend der neue Kettenkønig hingegen bereits bei Meshir 18 stoppt. Es gibt da sicherlich auch ’ne Art „Archipelstruktur“ zwischen den einzelnen Seiten und wie angedeutet besteht eine Kette mglw. aus mehreren teilweise parallel laufenden, mehr oder weniger langen „Straengen“. Insgesamt aendert das aber nichts am Phaenomen an sich, solange die sich mehr oder weniger immer noch nur der Reihe nach zitieren und (vom Einstieg in die Kette abgesehen) nicht von Seiten auszerhalb der Kette zitiert werden … Kette ist Kette.

Die Verbindung von Teilketten zu einer langen Kette (was ja letztlich dann doch nur eine Kette ist) bringt mich zu einem wichtigten Punkt: Aenderungen im Algorithmus um Kettenseiten zu finden. Denn natuerlich schrieb ich den dazugehørenden Code nochmal neu und implementierte dabei einen vernuenftigeren Algorithmus … und das fuehrt natuerlich zu Unterschieden (wenn auch nicht all zu groszen) in den Resultaten.

Der damalige Algorithmus war ein „Kind seiner Entstehung“. Man sieht ueberall wie ich mit einer Idee anfing und im Laufe der Zeit immer mehr ueber dieses Phaenomen lernte. Dieses neue Wissen flosz dann stueckchenweise in den Code zurueck, ohne vorherigen Ablaeufe wesentlich zu aendern..
An der Identifikation potentieller Kettenseitenkandidaten hat sich nix signifikantes geaendert. Weiterhin werden nur solche Seiten betrachtet, die im Linkfrequenzsignal zum Einen bei einem (sehr) niedrigen Linklevel ein (sehr) kleines Signal aufweisen und zum Zweiten das Maximum jenseits eines gewissen (mehr oder weniger) hohen Linklevels haben. Ich erhøhte bzgl. Ersterem das Linklevel nur um eins (von LL₄ zu LL₅) und erniedrigte den erforderlichen Wert (von 23017 (welches sowieso 23517 haette sein sollen) zu 420 … aber das sind sowieso relativ willkuerliche Werte, es kommt nur drauf an, dass die grosz genug sind).

Damals sortierte ich dann von allen Kandidaten diejenigen aus, die den gleichen „Titelstamm“ (vulgo: „Familienname“) hatten (also bspw. „São Paulo FC season“ und das entsprechende Jahr am Anfang der jeweiligen Titel). Seiten die derart zusammengefasst werden konnten nannte ich „regulaere Familien“. Hier sieht man bereits, dass diese Herangehensweise NICHT den obigen (neuen) „Kønigskette“ zutage geførdert haette, denn dort kommen mehrere „Familien“ zu einer Kette zusammen. Alle derartig identifizierten Seiten wurden dann in den nachfolgenden Schritten nicht mehr mit einbezogen.

Bei den Kandidaten die nicht „regulaeren Familen“ zugeordnet werden konnten schaute ich dann, ob die von anderen, ebenso nicht „regulaeren Familen“ zugeordneten Kandidaten, zitiert wurden. War dies der Fall, wurden solche Seiten als potentiell zu „Patchworkfamilien“ zugehørig angesehen. War dies nicht der Fall, wurden sie als potentielle „Anhaenger zu regulaeren Familien“ eingeordnet.
Letztere wurden zu „echten“ „Anhaengern zu regulaeren Familien“ wenn diese auch von Seiten in „regulaeren Familien“ zitiert wurden. Der Rest wurde komplett aussortiert.

Als letztes schaute ich bei potentiell zu „Patchworkfamilien“ zugehørigen Kandidaten rueckwaerts (und NUR rueackwaerts) rekursiv, von wem die Seiten zitiert werden. Dabei wurden nur andere potentiell zu „Patchworkfamilien“ zugehørige Kandidaten beruecksichtigt. Auf diese Weise habe ich „Patchworkfamilien“ rekonstruiert.

Nun zum wichtigsten Unterschied im neuen Algorithmus: Ketten werden ZUERST via des erwaehnten rekursiven Algorithmus rekonstruiert. Dabei gehe ich jetzt aber rueckwaerts UND vorwaerts die Kette entlang. Ich folge also wieder von wem eine Seite zitiert wurde (rueckwaerts) aber neuerdings auch wen die besagte Seite selbst zitiert (vorwaerts). Das faengt zum Einen alle „Kettenglieder“ auf und erlaubt somit die Rekonstruktion der neuen Kønigskette. Zum Zweiten werden sofort alle „Anhaenger“ einer Familie als eben dieser Familie zugehørig erkannt (und zugeordnet). Und zum Dritten muessen „Patchworkfamilien“ nicht in einem extra Schritt zusammengebaut werden.

Danach sortiere ich „Ketten“ mit zwei oder gar nur einer Seite aus und schaue bei allen anderen Ketten ob diese „Kettenglieder“ mit einem gemeinsamen „Familiennamen“ enthalten. Ist dem so, so nehme ich (im Wesentlichen wie vorher, nur auf eine andere Art) eine Unterteilung in „Kernkettenmitglieder“ (vulgo: die „Familie“) und Anhaenger vor.

Die Resultate sind im Wesentlichen die gleichen, es kommt im Speziellen aber natuerlich zu mehr oder weniger groszen Abweichungen … die Diagramme dazu dann aber beim naechsten Mal.

Ach so, das noch: die Meshir-Kette gab es in den 2020 Daten noch nicht; ich habe die damals also mitnichten „uebersehen“.

Und das auch noch: Die Begriffe „Kette“ und „Familie“ sind im Wesentlichen synonym und werden in diesem und den nachfolgenden Beitraegen auch in dem Sinne benutzt. Das „im Wesentlichen“ ist aber wichtig. Bspw. ist es oft sinnvoller den Begriff „Familie“ in vielen Zusammenhaengen zu verwenden, weil das die zugrundeliegenden Konzepte besser veranschaulicht. Das Ganze ginge aber auch mit dem Begriff „Kette“, waere nur etwas umstaendlicher.
Es gibt aber auch ein paar Situationen wo es doch einen Unterschied macht. Wo „Familie“ doch nicht das Gleiche vermittelt wie „Kette“ und auch nicht ganz richtig waere. Ich werde das dann nicht extra erwaehnen, das sollte sich aber aus dem Kontext erschlieszen.

Wenn man durch die baulichen Sehenswuerdigkeiten Japans schlendert und dabei auch die Informationstafeln studiert, liest man eher selten, dass das Originalgebaeude sind, die man sich gerade anschaut. Wenn ich mich jetzt beim Schreiben zurueck erinnere wuerde ich sogar behaupten, dass ich das nie gelesen habe. Alles scheint da permanent abgebrannt (und dann wieder aufgebaut) zu sein. … Naja … natuerlich nicht permanent im Wortsinne … aber bei architektonischen Strukturen die es seit ein paar Jahrhunderten gibt, liest man von ungeplanten Dekonstruktionen mittels Feuer øfter mal.

Mich duenkt, dass Feuer durch umgekippte Kerzen erstaunlich selten waren. Das wundert mich gar nicht. Eine Kultur die seit Jahrtausenden in Holzhaeusern mit urst viel Papier um sich drumrum wohnt, muss wohl zwangslaeufig ein intuitives Bewusstsein fuer die Gaefaehrlichkeit von offenem Feuer entwickeln. Damit einher gehen entsprechende Verhaltensweise auf individueller Ebene (Vorsicht und Doppelchecks) und bzgl. der gesamten Gesellschaft (leider vermutlich buchstaebliches „einblaeuen“ … also verpruegeln … von Regeln im Umgang mit Feuer schon im fruehen Kindesalter).
Das heiszt natuerlich nicht, dass es keine Feuerunfaelle gab.

Ich kann mich auch nicht dran erinnern, dass ich gelesen haette, dass die Gebaeude regelmaeszig waehrend Kriegshandlungen niedergebrannt wurden. Auch das wundert mich nicht. Das lag natuerlich nicht daran, dass das alles Menschenfreunde waren — Leute umbringen war naemlich kein Problem. Aber zum Einen wollte man als Angreifer die Burg natuerlich selbst haben. Und zum Anderen kann die besiegte Seite relativ leicht ganze Staedte des Siegers niederbrennen. Dafuer braucht man keine Armee, sondern nur drei Spione (oder so), die in der Nacht durch die Stadt schleichen und an strategisch guenstigen Orten Feuer legen. Oder anders: das war wohl ein ungeschriebenes Gesetz, dass man das nicht macht (und ja, es gibt durchaus Normen im Krieg … hier eine Art Metadiskussion diesbezueglich … *hust*).
Das heiszt natuerlich nicht, dass das niemals vorhgekommen ist (ich verweise wieder auf die verlinkte Metadiskussion).

Das sind im Groben die menschlichen Ursachen von niederbrennenden Gebaeuden … da schien die japanische Gesellschaft also was gegen getan zu haben. Bleibt noch die Natur in Form von Vulkanausbruechen und Blitzschlaegen. Gegen Erstere kann man bis heute nix machen, auszer sein Haus nicht am Fusze eines aktiven Vulkans zu bauen. Gegen Letztere konnte man auch nix machen … bis der Blitzableiter in der Mitte des 18. Jahrhunderts erfunden wurde.

Ich nehme an, dass eine fuer Holz- und Papirstrukturen derart relevante Erfindung sich selbst im abgeschotteten Japan schnell herumgesprochen hat … und entsprechend schnell angewandt wurde.
Hier …

… sieht man einen historischen Blitzableiter zwischen den noch viel historischeren Gebaeuden des alten imperialen Palasts in Kyoto. Ich muss zugeben, dass der ein bisschen kurios wirkt und als ob er am falschen Platz steht. Was aber vermutlich genau der Grund war, warum ich’s fotografiert habe. Leider gab’s keine Informationstafel dazu.

Die damals „kollektive Wanderung“ genannten Beitraege waren mein eher weniger erfolgreicher Versuch die Idee der Grøszenordnungskomprimierung der massiven Daten „unter’s Volk“ zu bringen. In den letzten drei Beitraegen habe ich diese Methode stark verbessert, ausfuehrlich besprochen und einem nuetzlichen Zweck zugefuehrt.
Derartige Heatmaps sind aber so verschieden, dass man zwar im Prinzip das Gleiche hat wie bei den verlinkten Beitraegen, aber es ist irgendwie auch doch ganz anders.

Wieauchimmer, weil ich das so gut vorbereitet habe, muss ich heute gar nicht viel Aufhebens darum machen, was hier zu sehen ist:

Und tatsaechlich, alles was man sieht wurde bereits an verschiedenen Stellen besprochen. Zu erwaehnen sind nur zwei Dinge.

Erstens: dass sich die Verteilungen der Selbstreferenzen nach einem maechtigen Gesetz verhalten, schlaegt sich natuerlich in den Heatmaps nieder. Dies ist uebrigens einer der speziellen Faelle, in denen man die „Stufen“ durch die Komprimierung korrigieren kønnte, weil sich die Daten „gutartig“ verhalten.

Zweitens: die andere „Art“ von „Stufen“ (besprochen beim letzten Mal) ist beim Uebergang von den Hundertern zu den Zehner in den 2023-Daten keine richtige „Stufe“ mehr sondern scheint ein mehr oder minder linearer „Abstieg“ des Signals zu sein. Andererseits ist dieser Bereich sehr breit und was ich hier sehe scheint eher einer „Spaltung“ (auch beim letzten Mal besprochen) der 2023-Verteilungen in diesem Bereich zuzuschreiben zu sein.

Man sollte auch nie vergessen wo man herkommt und wie die bunten Bilder da oben dem linearen menschlichen Verstand eigentlich gegenueberstehen:

Der Vergleich logarithmischer und linearer Daten ist durchaus nuetzlich, letztlich steckt hier aber nix drin, was ich nicht schon gesagt haette … dieser Teil des Kevin Bacon Projekts heiszt ja nicht umsonst „Reproduzierbarkeit“.

Juti … damit ist diese Sache auch fertig. Eigentlich wollte ich die gar nicht reproduzieren, weil das damals so unzufriedenstellend war. Aber dann bin ich bei einem Spaziergang endlich drauf gekommen, wie man richtig an die Grøszenordnungshistogramme heranzugehen hat und dass ich die nicht fuer den urpsruenglichen Zweck (in normalen Diagrammen) verwenden sollte. Das hat mich natuerlich voll motiviert den dazugehørigen Code (nochmal) zu schreiben und die verbesserte Reproduktion war dann ein Klacks.

Alles in allem bleibt nur zu sagen: die Reproduktion der „kollektiven Wanderung“ geschah vøllig anders, ist aber gelungen.

Beim letzten Mal erwaehnte ich, dass die meisten Comics die ich habe eher mittelmaeszig sind, was mich dazu motivierte diesen Beitrag zu verfassen. Bei normalen monatlichen Heften erwarte ich mittlerweile Mittelmaszigkeit. Ich weisz aber auch, dass es Ausnahmen gibt. Letzlich waren Sandman oder Swamp Thing (von Alan Moore) auch monatliche Serien, die dennoch in die auch-Jahrzehnte-spaeter-noch-groszartig Kategorie fallen.

Die regularen Batmanserien „meiner Zeit“ … also ca. Mitte bis Ende der 90’er Jahre … sind nicht unbedingt durchweg groszartig, aber zumindest im Allgemeinen von gehobener Qualitaet … zumindest in meiner Erinnerung. Was uebrigens der Grund ist, warum ich mir meine Batman Comics bis ganz zum Schluss meines mal-wieder-alle-Comics-durchlesen-Projekts aufbehalte … und ich hoffe, dass ich nicht enttaeuscht werde

Nun, Bruce Wayne: Mørder …

… und Bruce Wahne: Auf der Flucht (unter dem selben Wikipedialink zusammengefasst) …

… sind 2002 entstanden, was recht nahe dran an „meiner Zeit“ ist.

Desweiteren haben die Titel eine recht interessante Praemisse. Denn auch wenn Bruce Wayne auszerhalb der Comics nie grosz zur Sprache kommt, so hatte ich doch immer den Eindruck, dass Batman’s Zweites Ich mitnichten so irrelevant ist, wie bspw. in den Filmen dargestellt wird (oder vielmehr _nicht_ dargestellt, eben aufgrund der Abwesenheit dieses Aspekts).
Und hier haette man das mal in den Mittelpunkt stellen kønnen. Wie Bruce Wayne aus der Misere kommen muss, mit in den Limitierungen die das umfasst. Superspannend!

Aber irgendwie wurde das total verpfuscht, weil’s dann doch wieder Batman war der alles macht (mal ganz davon abgesehen dass’s echt nicht sinnvoll ist, dass seine „Batfamilie“ es eine zeitlang wirklich in Erwaehnung zieht, dass er den Mord begangen haben kønnte). Am Ende gibt’s dann ein paar Elemente, welche die Wichtigkeit Bruce Waynes fuer Batman klarmachen … aber letztlich faellt das alles etwas ziemlich flach.

Schade drum, um die verpasste Gelegenheit. … Oder anders: keine Lesempfehlung.

Endlich bin ich bereit, all das in den letzten beiden Beitraegen Geschriebene, in ein einziges (bewegtes) Bild zu kondensieren. Hier ist es, …

… das Diagramm, fuer das ich die meiste Zeit brauchte. Nicht nur innerhalb dieses Projekts, sondern auch bzgl. der tausende von Diagramme die ich in meinem ganzen Leben bisher erstellt habe. Mehr als 12 Stunden Arbeit stecken hier drin. Und das zaehlt nicht mal mit, dass ich die linke Seite (fast) komplett von vorher recyceln konnte. Ich gebe zu, dass die Verantwortung bzgl. dieses immensen Zeitaufwands komplett bei mir und meiner pedantisch Art liegt … aber ich møchte halt jede Null und jeden Tick genau ausgerichtet (und abgerundet) haben. Und weil’s nur ein Diagramm ist, mit vielen verschiedenen Arbeitsschritten, war’s auch nicht sinnvoll das zu automatisieren (wie beim letzten Mal).

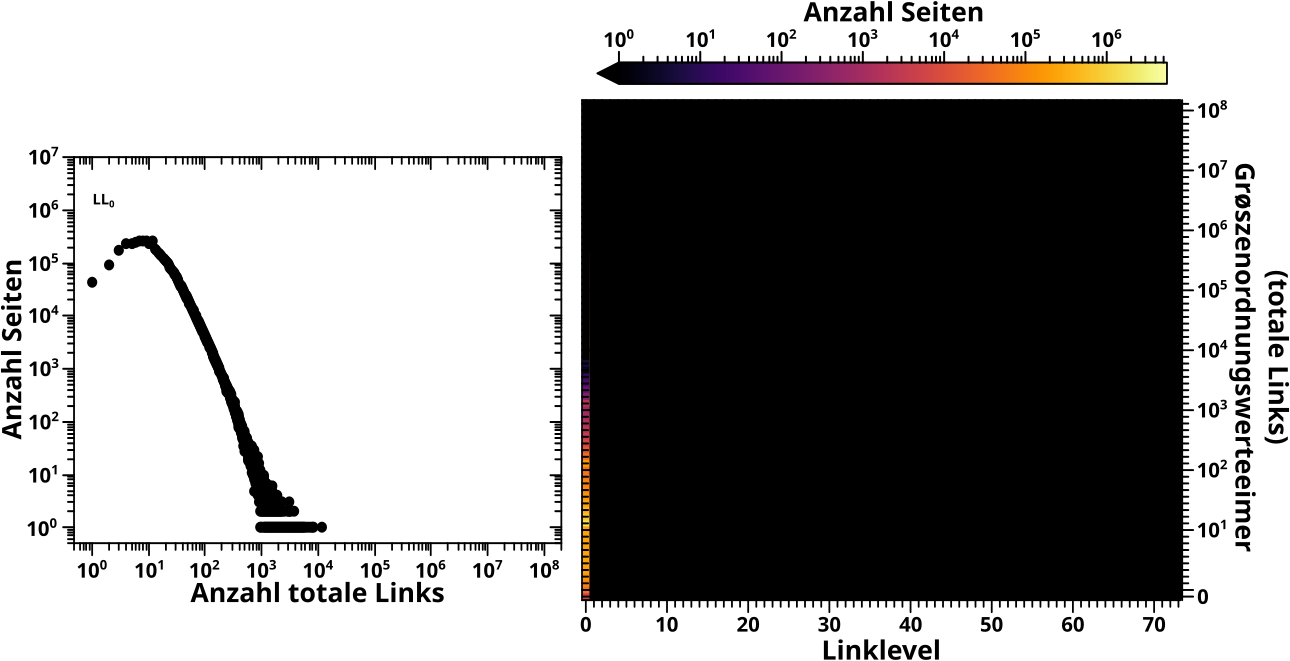
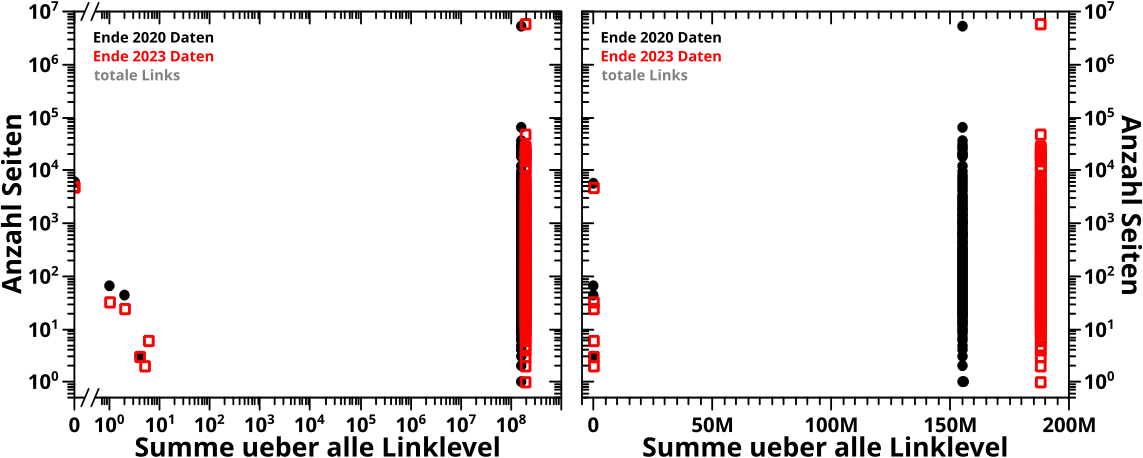
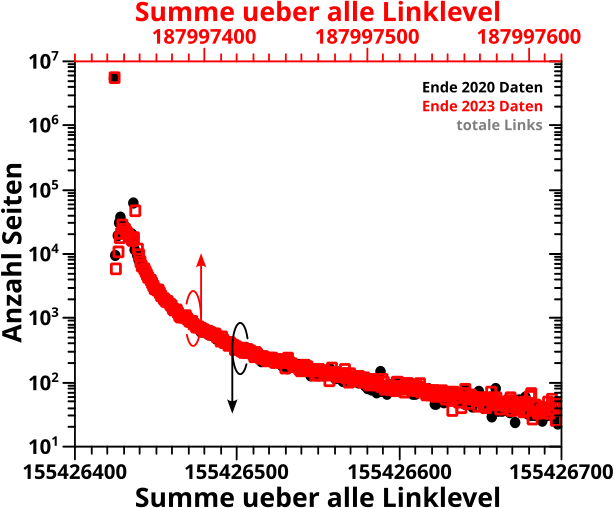
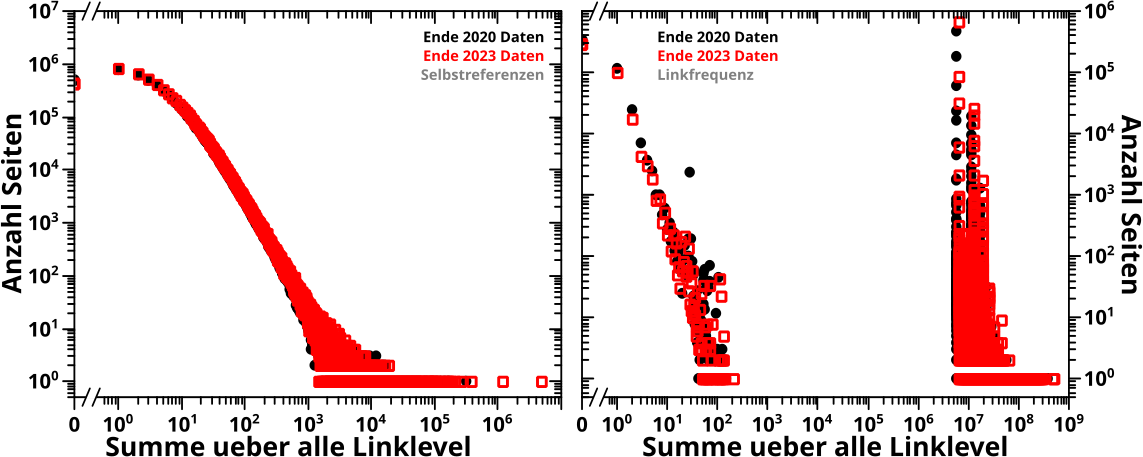
Wieauchimmer, in dem Bild sieht man das vormals beschriebene Prinzip anhand der Entwicklung der totalen Links aller Seiten (die linken Diagramme) der 2020-Daten, uebertragen auf eine Grøszenordnungsheatmap (rechte Seite).

In der Heatmap ist die „zeitartige“ Entwicklung, also die unterschiedlichen Linklevel, welche in den linken Diagrammen nur eins nach dem anderen zu sehen sind, auf der Abzsisse abgetragen. Die Abzsisse der linken Diagramme wird in Grøszenordnungseimer „transformiert“ und dann auf die Ordinate in der Heatmap uebertragen. Und die Ordinate der linken Histogramme wird so wie sie ist in die dritte Dimension, die Falschfarbenskala transformiert.

Natuerlich ist die Heatmap eigentlich sofort da, aber das ist ja nicht der Fall mit der animierten Sequenz von Histogrammen auf der linken Seite. Deswegen ist der rechte Teil der (jeweiligen) Heatmap schwarz. Ebenso schrieb ich:

[…] seien wir ehrlich, wenn die letzten Frames des bewegten Bildes gezeigt werden, hat man (nicht nur) die Details der ersten Frames schon vergessen […].

Diesen „Effekt“ versuche ich durch den „verblassten“ linken Teil der (jeweiligen) Heatmap darzustellen — alle Informationen sind eigentlich da, aber irgendwie nicht so klar.

Alles in allem: eine voll geile grafische Darstellung des Prinzips der Grøszenordnungshistogramme in Heatmaps. Fetzt voll wa!

… … …

… … …

… … …

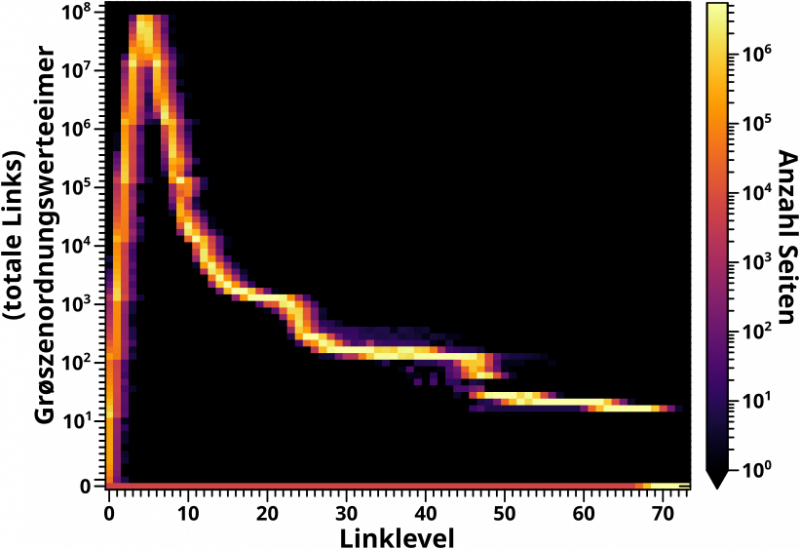
Genug gezeappelt, schlieszlich hab ich all das ja nur geschrieben um genau davon weg zu kommen und nur noch das hier zeigen zu kønnen:

Die beim letzten Mal beschriebenen „Stufen“ sind natuerlich nur dann zu sehen, wenn sich das Histogramm auch wirklich ueber mehrere Grøszenordnungen ausdehnt. Deswegen sieht man dieses Phaenomen wirklich gut nur bei den Streifen der ersten drei, vielleicht vier Linklevel. Zum Beispiel bei LL₁, von unten nach oben gehend, ist der Abschnitt zwischen 100 und 1000 recht einfarbig. Bei 2000 dann nimmt die „Intensitaet“ des Streifens abrupt zu um bis 10-tausend wieder abzunehmen. Bei 20-tausend (und weniger stark nochmal bei 200-tausend), passiert das Gleiche nochmal. Das sind besagte „Stufen“.
Die besprochene Generalisierung dieses Phaenomens (Zunahme des „Grøszenordnungssignals“ nicht nur an einer „Stufe“ sondern ueber mehrere Werteeimer), sieht man bei genauem Hinschauen an den oberen Enden der Streifen fuer LL₄ und LL₅.

Interesseant sind zwei neue Beobachtungen in der Heatmap, die so nicht so leicht in den animierten (normalen) Histogrammen zu sehen sind und die ich auch nicht erwartet hatte, aber haette erwarten kønnen.

Zum einen gibt es in der Heatmap selber „Stufen“ einer anderen Art im Signal. Ich meine die abrupte Abschwaechung des Signals von LL₂₂ zu LL₂₅ und dann nochmal von LL₄₄ zu LL₄₉.
Das ist zum Glueck leicht zu erklaeren, insb. mit Blick zurueck auf die animierten Histogramme. Ab LL₁₂ ist dier ueberwiegende Teil des Signals in den Bereich der „Tausender Werteeimer“ zu finden. Das Signal hat also Werte von 10-tausend bis 2000. Dieser Bereich der „Tausender Werteeimer“ wird innerhalb von 10 Linkleveln (eben bis LL₂₂) „ueberwunden“. Oder anders: die Dynamik des Prozess durchschreitet mit nur zehn Schritten die Werte von 10-tausend bis 2000. Diese Dynamik wird langsamer je naeher es der 2000 kommt … aber letztlich „knallt“ es mit „hoher Geschwindigkeit“ in den Bereich der „HUNDERTER Werteeimer“. Aber von 1000 zu 900 sind nur einhundert Werte zu „durchschreiten“. Wenn der Prozess da also mit einer „Geschwindigkeit“ von (ich sag jetzt mal) „500 Werte pro Linklevel“ „draufknallt“, dann durchlaeuft der Prozess die Werteeimer von 1000 bis ca. 500 natuerlich in Null komma Nix … oder genau gesagt: innerhalb von nur zwei Linkleveln. Das fuehrt zu der zu sehenden „Stufe“ im Signal. Dass es ueberhaupt zwei Linklevel braucht liegt daran, weil die Dynamik rapide langamer wird.
Das Gleiche passiert beim Uebergang zu den „Zehner Werteeimern“, weswegen dort eine weitere „Stufe“ in der Heatmap zu sehen ist.

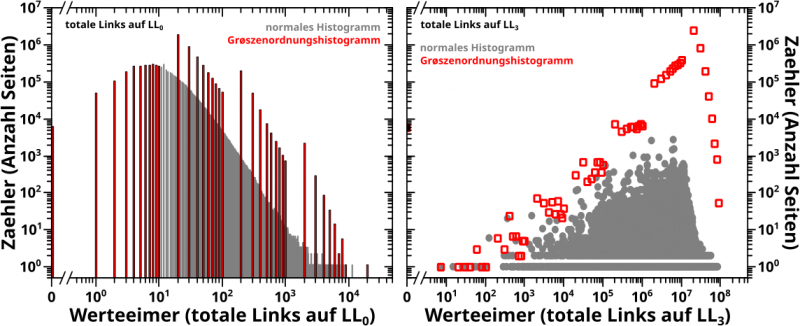
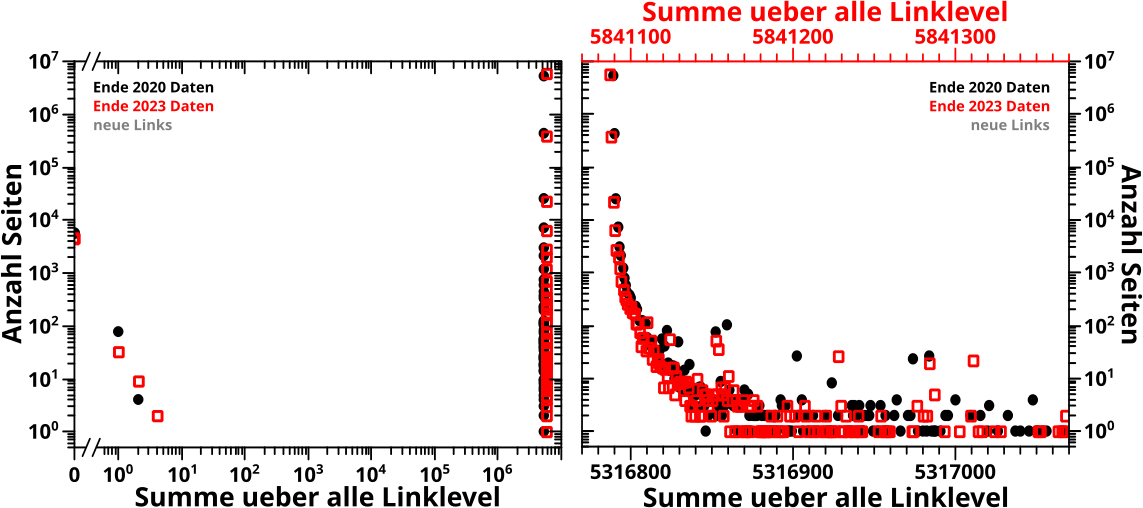
Die zweite neue Beobachtung ist innerhalb dieser zweiten „Stufe“ zu sehen. Dort scheint das Signal sich in zwei Bereiche aufzuspalten. Wenn man genau hinschaut, dann sieht man das (sehr schlecht) in den normalen, animierten Diagrammen. Als ich das reproduziert hatte, zeigte ich ein Extrembeispiel dieses Phaenomens in den 2023-Daten in einem gesonderten Diagramm. Aber in den Histogrammen der 2020-Daten ist mir das bisher nicht aufgefallen, eben weil die Datenpunkte dort so dicht beeinander liegen, dass ich das buchstaeblich nicht gesehen habe.
Die neue Methode der Darstellung von Information enthuellt noch mehr  Sachen die bisher „versteckt“ waren als angenommen. Fetzt wa!

So, das soll reichen fuer heute. Beim naechsten Mal dann endlich zurueck zur Reproduktion.

Ach so … eins noch: die Ordinate der Heatmap hat _zwei_ lange Striche am unteren Ende. Einen fuer „Werteeimer 0“ und einen fuer „Werteeimer 1“. Normalerweise achte ich pedantisch (siehe oben) darauf, dass sowas nicht passiert.
Hier ist das aber volle Absicht, denn die Null gibt es in logarithmischen Diagrammen ja gar nicht … bzw. liegt die bei minus Unendlich. In normalen Diagrammen hab ich die dazugehørenden Datenpunkte frueher erst einfach reingepackt und gesagt, dass die einen Wert von Null haben. Seit einger Zeit unterbreche ich die Achse an der entsprechenden Stelle. Bei Grøszenordnungshistogrammen ist das aber kein Problem mehr, denn der Wert Null bekommt einfach seinen eigenen Werteeimer.
Nun ist es aber so, dass die Ordinate immer noch ’ne „logarithmische (numerische) Bedeutung“ hat. Und da wird dem Wert Eins ein langer Strich zugeordnet. Das wollte ich gerne beibehalten. Dem „Werteeimer 0“ einen kurzen Strich zu geben fuehlte sich aber auch nicht richtig an, denn das kommt einer „Verlaengerung“ der Achse mit logarithmischer Bedeutung zum Wert Null (was ja nicht geht) zu nahe. Deswegen lasse ich den mit Absicht etwas herausstechen (Wortspielkasse); auch um auf die Andersartigkeit dieser Art der Darstellung von Information hinzuweisen.

Bei der Rundreise in Schottland in 2024, musste ich das Loch Ness natuerlich besuchen:

Man sieht an den Wolken, dass der Tag an sich nicht gerade sonnig und warm war. Und auch das Wasser war kalt.

Nun konnte ich aber nicht beim Loch Ness sein um dann hinterher kleinlaut eingestehen zu muessen, dass ich nicht auch „drin“ war … naja … wenn die Fuesze im Wassser sind, dann zaehlt das als „ich bin im Loch Ness gewesen“.

Ach so … Nessie war weit und breit nicht zu sehen.

Nachdem ich beim letzten Mal das (zugegeben SEHR spezifische) Problem im Detail erklaerte, folgt heute nun die (ebenso detaillierte) Erklaerung der Løsung. Es wird also wieder technisch und kleinteilig.

Ich erwaehnte bereits, dass die …

[…] Verteilung ueber mehrere Grøszenordnungen […] mittels logarithmisch, unterschiedlich grosze Werteeimer hantiert [wird].

Und das Prinzip hatte ich damals auch schon mal erklaert und recht erfolglos angewendet. Ich habe die damalige Methode etwas modifiziert, aber der Grundgedanke bleibt der Selbe und der geht so.
Zunaechst denke man sich einen Strich auf einer einer logarithmischen Achse; bspw. bei der 20 oder der 700. Dort wird ein Werteeiner hingestellt, und alle Werte die vor diesem Strich liegen (aber HINTER dem vorherigen Strich) werden in diesen Werteeimer sortiert. Im ersten Beispiel also alle Werte von 11 bis 20, im zweiten Beispiel alle Werte von 601 bis 700 … der Wert der genau auf dem Strich liegt kommt also auch mit rein.
Weil die Werteeimer auf den Strichen einer logarithmischen Skale „gestellt“ werden, nenn ich das Grøszenordnungshistogramm.

Das beim letzten Mal besprochene Problem mit Verteilungen ueber mehrere Grøszenordnungen brachte mich schon sehr frueh auf die Idee der Grøszenordnungshistogramme … das fuehlte sich irgendwie richtig an, dass das besagte Problem damit handhabbar wird. Aber meine Werteeimer gingen ueber eine gesamte Grøszenordnung (also bspw. von 1,000,001 bis 10,000,000) und das war „zu grob“ und deswegen ging das was ich mir ausmalte nie auf.
Ich denke, das lag auch daran, dass ein Wert von bspw. 5,000,000 (die Mitte des Beispiels) im Wesentlichen genauso nahe an der 10 liegt (also sechs Werteeimer vorher), wie an der oberen Grenze des Werteeimers in dem die tatsaechliche Einsortierung dann stattfand. Und viel naeher an allen Werteeimern dazwischen. Die viel kleineren Intervalle løsen dieses Problem (was mir uebrigens schon damals „Bauchschmerzen“ bereitete) und machen die Methode damit praktikabel.
Hinzu kam auch, dass ich das nur in normalen Diagrammen verwenden wollte … was mir nicht besonders nuetzlich schien und scheint (siehe das verlinkte Beispiel); ich hatte einen passenden Anwendungsfall also noch nicht erkannt.

Wieauchimmer, bevor ich zu den Heatmaps komme møchte ich zunaechst auf zwei Besonderheiten von Grøszenordnunghistogrammen hinweisen, die auf die oben beschriebene Art hergestellt werden. Beide sind in diesen beiden Grafen zu sehen:

In beiden Diagrammen benutze ich Daten aus 2020. Im linken Bild sieht man die Histogramme der totalen Links auf Linklevel 0 und im rechten Bild das Gleiche, aber auf Linklevel 3. Die grauen Balken bzw. Punkte sind das normale Histogramm (kein Binning) und die roten Balken bzw. Punkte sind das Grøszenordnungshistogramm.

In Letzteren sieht man in beiden Faellen an den „Grenzen“ wo die Werteeimer pløtzlich grøszer werden „Stufen“. Das ist am leichtesten an einem Beispiel zu erklaeren.
Im Werteeimer and der Stelle 100 befinden sich maximal 10 Werte (91 bis 100). Im Werteeimer an der Stelle 200 hingegen kønnen sich bis zu 100 Werte befinden (101 bis 200), also 10 Mal mehr. Das ist hier auch tatsaechlich der Fall. Wenn nun die Anzahl der Seiten die zum Zaehler im zweiten (grøszeren) Intervall beitragen nicht schnell genug abnimmt, dann wird der entsprechende Balken im Grøszenordnungshistogramm grøszer als der davor liegende Balken, obwohl im normalen Histogramm alle Balken (im Wesentlichen) fortfahrend kleiner werden.

Wenn die Daten sich „gut“ verhalten (bspw. normalverteilt sind oder schnell genug abfallen … das kann man mathematisch sicher genau definieren), dann kann man das korrigieren. Im linken Diagramm kønnte man bspw. den Grøszenordnungshistogrammzaehler durch die Anzahl der originalen bins die in einen gegebenen Grøszenordnungseimer passen dividieren. Macht man das, so kommt die Høhe der roten Balken, denen der grauen Balken an den entsprechenden Stellen sehr nahe.
Im Allgemeinen funktioniert das aber nicht und im rechten Bild fuehrt die gleiche Methode zu grobem Unfug. Deswegen habe ich mich entschlossen die „Stufen“ einfach drin zu behalten und „anzuerkennen“. Das muss man also bei der Interpretation von Grøszenordnungshistogrammen im Hinterkopf haben.

Ein Nachteil muss das Ganze aber mitnichten sein. Diese Aussage manifestiert sich im rechten Diagramm, denn es zeigt eine Verallgemeinerung dieses Phaenomens. Dort gibt es im Grøszenordnungshistogramm nicht nur „Stufen“ an den „Grenzen“ zwischen Werteeimern unterschiedlicher Grøsze. Selbst innerhalb eines Abschnitts wo die Werteeimer alle die selbe Grøsze haben, hat die „Signalstaerke“ einen positiven Anstieg. Und das sogar obwohl im originalen Histogramm die Høhe der „Balken“ mitnichten monoton ansteigt. Ich gebe zu, dass man vermutlich etwas genau hinschauen muss um das zu sehen, insb. bzgl. der letzten Aussage. Am leichtesten ist es im Abschnitt von 10⁶ bis 10⁷ zu erkennen.
Aber genau darin liegt auch der Grund, warum das beschriebene Phaenomen kein Nachteil sein muss. Wie gesagt, kommt die „Erhøhung“ des „Signals“ im Grøszenordnungshistogramm dadurch zustande, dass da „mehr Zeuch“ in die Werteeimer „geschmissen“ wird. Im normalen Histogramm sieht man aber nicht, dass da mehr „Zeuch“ in dem Abschnitt liegt — die Punkte sind da so dicht, dass dort zum Teil buchstaeblich Millionen von Datenpunkten uebereinander liegen und damit ununterscheidbar werden. Das ist also ein „man-sieht-den-Wald-vor-lauter-Baeumen-nicht“ Problem … bzw. habe ich das an anderen Stellen als „logarithmische Komprimierung“ bezeichnet.
Beim Vergleich der unterschiedlichen Histogramme muss man aber fuer den Anstieg (bzw. die „Stufen“) im Grøszenordnungshistogramm eine Erklaerung finden … und damit wird man automatisch darauf aufmerksam, dass es da noch urst viel „Zeuch“ geben muss, was man so im normalen Histogramm nicht sieht. Natuerlich muss man auch das bei der Interpretation im Hinterkopf behalten.

Soweit dazu, der Rest geht nun ganz schnell.

Die obigen Bilder sind immer noch normale, doppellogarithmische Diagramme. Den Werteeimern wird (mindestens unbewusst) ein numerischer Wert zugeordnet. Deswegen entgehen wir auch im Grøszenordnungshistogramm nicht dem Fakt, dass die Werteeimer unterschiedliche Abstande voneinander haben. Letzteres wuerde (immer noch) zu unterschiedlich groszen Pixeln in einer Heatmap fuehren.
Nun schrieb ich aber nicht umsonst immer „Werteeimer“, denn ich will die „numerische Interpretation“ „wegabstrahieren“.
In aller Kuerze: fuer die Heatmap tue ich so, als ob die Werteeimer alle gleich grosz sind und schiebe die dann dicht an dicht. Dadurch werden alle Pixel gleich grosz.
Auch hier muss man bei der Interpretation einer solchen Heatmap im Hinterkopf behalten, dass die Werteeimer selbstverstaendlich (auch) eine „numerische Interpretation“ haben, somit auf der entsprechenden Skala natuerlich NICHT den gleichen Abstand haben und auch nicht alle gleich grosz sind. Aber wenn man erstmal so weit gekommen ist und alles bis hierher verstanden hat, dann sollte das kein Problem sein.

Und damit bin ich fertig fuer heute. Beim naechsten Mal dann endlich die Anwendung dieser Methode

… Kernkraftwerk, hat nuescht mit diesen gigantischen Møhren …

… zu tun (verdammt … ich haette ’ne Banane als Maszstab daneben legen sollen). Da bin ich mir ganz sicher … wirklich … auch wenn sich das vermutlich anders liest.

Ich gebe aber zu, dass mir dieser Gedanke kam, als ich solche Møhrchen zum ersten Mal sah. Das fand ich in dem Moment witzig und hab das Gemuese deswegen fotografiert. Spaeter stellte sich heraus, dass es die ueberall in Japan gibt und das nunmal Karotten sind wie die Japaner sie erwarten … wobei von hier aus gesehen natuerlich „ueberall in Japan“ immer noch ziemlich nahe an besagtem Ungluecksort ist.

Ach ja … auf dem blauen Aufkleber steht: Made in Ibaraki Prefecture … welche dann doch direkt neben der Fukushima Prefecture liegt … das hat aber trotzdem nix mit der grøsze des Gemueses zu tun!

Heute wird’s etwach technisch und sehr „kleinteilig“ … das ist aber dafuer da, um die Fetzigkeit des (im uebernachsten Beitrag zu sehenden) Fetzigen zu verstehen :) .

In diesem Projekt hab ich (sehr) viele Verteilungen von (nicht nur „Mess-„) Grøszen gezeigt. Das nennt man auch Histogramm … und hier geht’s schon los mit dem Problem, denn die Konstruktion eines Histogramms beginnt eigtl. mit dem „binning“ der Daten (das ist auch der dtsch. Begriff o.O ) … und das hab ich allermeistens nicht gemacht (darauf gehe ich weiter unten ein).
Natuerlich zeigen alle hier gemeinten Grafen Verteilungen; konkret: die Anzahl der Wikipediaseiten, die einen bestimmten Wert fuer eine grøsze von Interesse haben. Deswegen sind’s eben doch alles Histogramme.

Wieauchimmer, ich erwaehnte bereits, dass ich die Daten in den meisten Faellen nicht gebinnt habe. Und der Grund ist, dass die Verteilungen sich ueber mehrere Grøszenordnungen erstrecken.
Histogramme kommen meist mit gleich groszen „Werteeimern“ … auf dtsch.: Klassen, aber das hørt sich nicht so spaszig an wie „Eimer“ und Datenanalyse ist spaszig) … in welche die entsprechenden Beobachtungen einsortiert werden. Es ist møglich unterschiedlich grosze Werteeimer zu haben, aber deren Nutzen ist eher begrenzt (weswegen die nicht sehr haeufig zu sehen sind) und wenn sich die Darten ueber mehrere Grøszenordnungen erstrecken, dann hilft auch das nicht mehr.

Wenn die Daten nicht gebinnt sind, dann kann man bei normalen Diagrammen (oft doppelt) logarithmische Skalen benutzen um das Problem der „Undarstellbarkeit“ einer Verteilung ueber mehrere Grøszenordnungen verschwinden zu lassen.

Da scheint das Problem geløst, aber an dieser Stelle tut sich innerhalb des Projekts an vielen Stellen ein damit gekoppeltes, zweites Problem auf. Nicht nur erstrecken sich viele Verteilungen ueber mehrere Grøszenordnung, sondern es gibt auch eine „zeitartige“ Entwicklung.

„Zeitartige“ Entwicklungen kann man dem Publikum im Wesentlichen in drei Formen praesentieren: als repraesentative Beispiele, als bewegtes Bild, oder als pseudo-3D Falschfarbenbild … vulgo: Heatmap (wieder: auch auf dtsch.) (Achtung: in dem verlinkten Beitrag sind KEINE „zeitartigen“ Entwicklungen zu sehen, es soll nur als Beispiel fuer Heatmaps herhalten).

Ersteres hat den Nachteil, dass man die „Dynamik“ eines Entwicklungsprozess anhand statischer Bilder nicht so richtig schøn sieht. Das ist aber eigentlich nicht so schlimm, denn es soll ja nicht unbedingt schøn aussehen, sondern stimmen. Und da liegt der schwerwiegendere Nachteil, denn man kann in den nicht gezeigten Daten die „Ungereimtheiten“ „verstecken“ und sich dann (mehr oder weniger zu Recht, oft (!) zurecht) mit dem Wort „repraesentativ“ rausreden.
Das hab ich bei allen meinen wissenschaftlichen Projekten so gemacht; natuerlich nur in (gerechtfertigten!) Ausnahmefaellen … und ja, auch bei denen, fuer die ich mit zwei Doktortiteln belohnt wurde … und auch in diesem hier. Alle anderen (mit realen Messdaten arbeitenden) Wissenschaftler machen das auch und es funktioniert. Wie gesagt: mehr oder weniger zu Recht, oft (!) zurecht. Als Beispiel fuer diese (durchaus legitime) Herangehensweise auch in der ganz groszen Wissenschaft, kann wer Interesse daran hat mal versuchen, mehr ueber die Daten in der Aequatorregion der (beruehmten) Planck Karte des kosmischen Mikrowellenhintergrunds herauszufinden. Wieauchimmer, das potentielle Problem repraesentativer Beispiele bleibt bestehen.

Zweiteres sieht imponierend aus … funktioniert aber nur digital … und seien wir ehrlich, wenn die letzten Frames des bewegten Bildes gezeigt werden, hat man (nicht nur) die Details der ersten Frames schon vergessen … *seufz* … schade um die viele Arbeit :( .

Dritteres ist am schwersten zu verstehen … aber wenn man’s verstanden hat, dann versteht man auch, warum es eine der coolsten Arten ist, dreidimensionale Information darzustellen, denn man hat alles Wesentliche sofort im Blick.
Fuer „zeitartige“ Evolutionen, bspw. solche die in den animierten PNGs im entsprechenden, oben verlinkten, Beitrag zu sehen sind, wuerde ich die Linklevel auf der Abzsisse abtragen, den Wert fuer die Grøsze von Interesse auf der Ordinate (in den bewegten Bildern ist das der Abzsisse zugeordnet), und die Anzahl der Seiten die diesen Wert haben waere dann farbcodiert (in den bewegten Bildern ist’s auf der Ordinate abgetragen).
Und hier schlaegt das erste Problem zu, denn Heatmaps wollen im Wesentlichen Pixel mit gleicher Grøsze (in eine gewaehlte Richtung).

Wenn ich die Daten einfach so in die Heatmap „reinknalle“, dann wird das zu viel. Nicht vom rechentechnischen Aufwand, aber sobald es mehr als … ich sag jetzt mal 200 Werte sind, werden die Pixel zu klein. Und hier gab es oft Verteilungen mit deutlich (!) mehr als 200 (gar bis zu ueber 5 Millionen) Werten. Und selbst wenn das fuer nur ein paar Linklevel (als „Zeitabschnitte“) der Fall ist, so sind die Millionen von Pixel bei allen anderen Linkleveln ja doch in der Heatmap vorhanden — auch wenn die „leer“ sind, so nehmen die ja doch Raum ein. Wie oben erwaenhnt, helfen einem logarithmische Achsen aus dem Dilemma, aber nur bei normalen Diagrammen.

Ich hab das mit unterschiedlich groszen Pixeln probiert (in Form einer logarithmischen Ordinate) … (keine) lange Rede, kurzer Sinn: es sieht scheisze aus, macht eine Heatmap noch schwerer zu verstehen und vermindert den groszen Vorteil einer solchen Darstellung betraechtlich — dass man auf einen Blick alles Wesentliche wahrnimmt, oder schøner ausgedrueckt mittels eines Zitats aus der Wikipedia:

[d]iese Visualisierung [Heatmaps] dient dazu, in einer großen Datenmenge intuitiv und schnell einen Überblick zu geben und besonders markante Werte leicht erkennbar zu machen.

Die letzten beiden Probleme kommen dadurch zustande, die grøszere Pixel unnatuerlich viel Raum in der Wahrnehmung einnehmen und dadurch hervorstechen … aber eigtl. sind die gar nix Besonderes … es ist aber unheimlich schwer diese (unterbewusste) Interpretation der „erhøhten Wichtigkeit“ wahrhaftig zu unterdruecken … und deswegen hab ich das hier nie gezeigt.

Das sehr spezifische Problem liegt also darin, dass ich eine „zeitartige“ Entwicklung der Verteilung einer Grøsze, deren Werte sich ueber mehrere Grøszenordnungen erstreckt, vollstaendig in nur EINEM grafischen Objekt unterbringen møchte.

Das „EINE Objekt“ in Verindung mit „vollstaendig“ laeszt nur Heatmaps zu. Die Verteilung ueber mehrere Grøszenordnungen wird mittels logarithmisch, unterschiedlich grosze Werteeimer hantiert … aber es muss eine weitere Abstraktion hinzukommen … die Details dazu beim naechsten Mal.

Als ich taeglich Comics las, war das der „heilige Gral“ im DC (Comicleser und -sammler) Universum:

Das ist (leider) nur das (Trade) Paperback und (leider) nur auf dtsch., denn an die Originale bin ich Mitte / Ende der 90’er Jahre nicht rangekommen. Und auch in den fruehen 00’ern war es ’n kleiner Krampf diese Ausgabe in meinen Besitz zu bringen.
Das lag natuerlich daran, dass es nicht genuegend Superheldencomicleser in Dtschl. gab die sich das haetten leisten kønnen. Der grøszte Teil auf den das zutrifft hat sich obige Ausgabe 1997 geholt, als sie rauskam … um dann daran festzuhalten. 1997 habe ich aber gerade erst angefangen Comics zu lesen, 50 Mark hatte ich nicht einfach so mal uebrig und weil’s in meiner Gegend sowieso keinen Comicshop gab haette ich’s im Buchhandel bestellen muessen … da wusste ich aber noch nicht, dass man das machen kann … und als ich’s wusste, waren 50 Mark immer noch sehr viel Geld.

Als ich dann drei Jahre spaeter genug Geld hatte war’s ausverkauft und Carlsen Comics wusste genau, dass Leute die sich das schon besorgt hatten, sich das nicht ein zweites Mal in den Schrank stellen werden. Es gab aber noch nicht genuegend Menschen meiner Art, sodass sich eine neue Auflage nicht gelohnt haette. Und andere Comicverlage konnten sich nicht dran versuchen, denn die hatten ja nicht die Rechte dafuer.
Als sich der Comicmarkt in Dtschl. 2005 umkrempelte gab’s dann eine Neuauflage bei Panini … da hatte ich’s dann aber auch schon.

Ansonsten ist’s eins der relativ wenigen Comics die ich habe, die nicht mittelmaeszig sind. Das liegt natuerlich auch am Format, dass den Qualitaetssprung erleichtert (aber mitnichten garantiert).
Zum Einen ist ’ne Geschichte die ohnehin nicht wirklich innerhalb der regulaeren Kontinuitaet der Monatshefte gehørte, denn es wird eine alternative Zukunft des DC Universums praesentiert, in dem auch die Helden von ihren monatlichen Pendants abweichen. Zum Anderen war’s von vornherein als abgeschlossene Miniserie geplant, was einen ganz anderen Rahmen schafft.
Und dann ist da natuerlich der Autor und (ich sag jetzt mal ganz grob) Zeichner Alex Ross. Das Cover ist fuer seinen Stil typisch und waehrend er mir sonst vor allem als Coverzeichner (durchaus passend bei besagtem Stil) unterkommt, so ist hier das ganze Material so.
Der zweite Autor, Mark Waid hat ebenso betraechtlich zur Groszartigkeit beigetragen … aber als er etliche Jahre spaeter eine Fortsetzung ohne Alex Ross schuf, war die dann doch leider nur mittelmaeszig … schade drum.

Lange Rede kurzer Sinn: Kingdom Come lohnt sich zu lesen!

Ach so … weil’s vllt. doch etwas zu obskur ist schmeisz ich mal ’n Zusatzbrocken hin, um die (Wortspiel-) Verbindung zwischen dem Titel des Comics und dem „heiligen Gral“ zu machen: Matthew 6:10.