Søren in Norwegen

Beim letzten Mal verwies ich auf einen aelteren Beitrag, der nicht nur die beim letzten Mal (mehr oder weniger) reproduzierten Reaktivierungen pro Linklevel zeigte, sondern auch zwei tolle bunte Bilder.

Im ersten bunten Bild untersuchte ich wie lange (in „Linkleveleinheiten“) es dauert von einer Reaktivierung der Selbstreferenzen bis zum naechsten „Ausstieg“. Dabei ist zu beachten, dass

[e]ine Kette an Selbstreferenzen […] mehrfach abbrechen und reaktiviert werden [kann].

Ich nannte das damals „Selbstreferenzenketten“ … und nenne das jetzt lieber „Reaktivierungslaenge“.

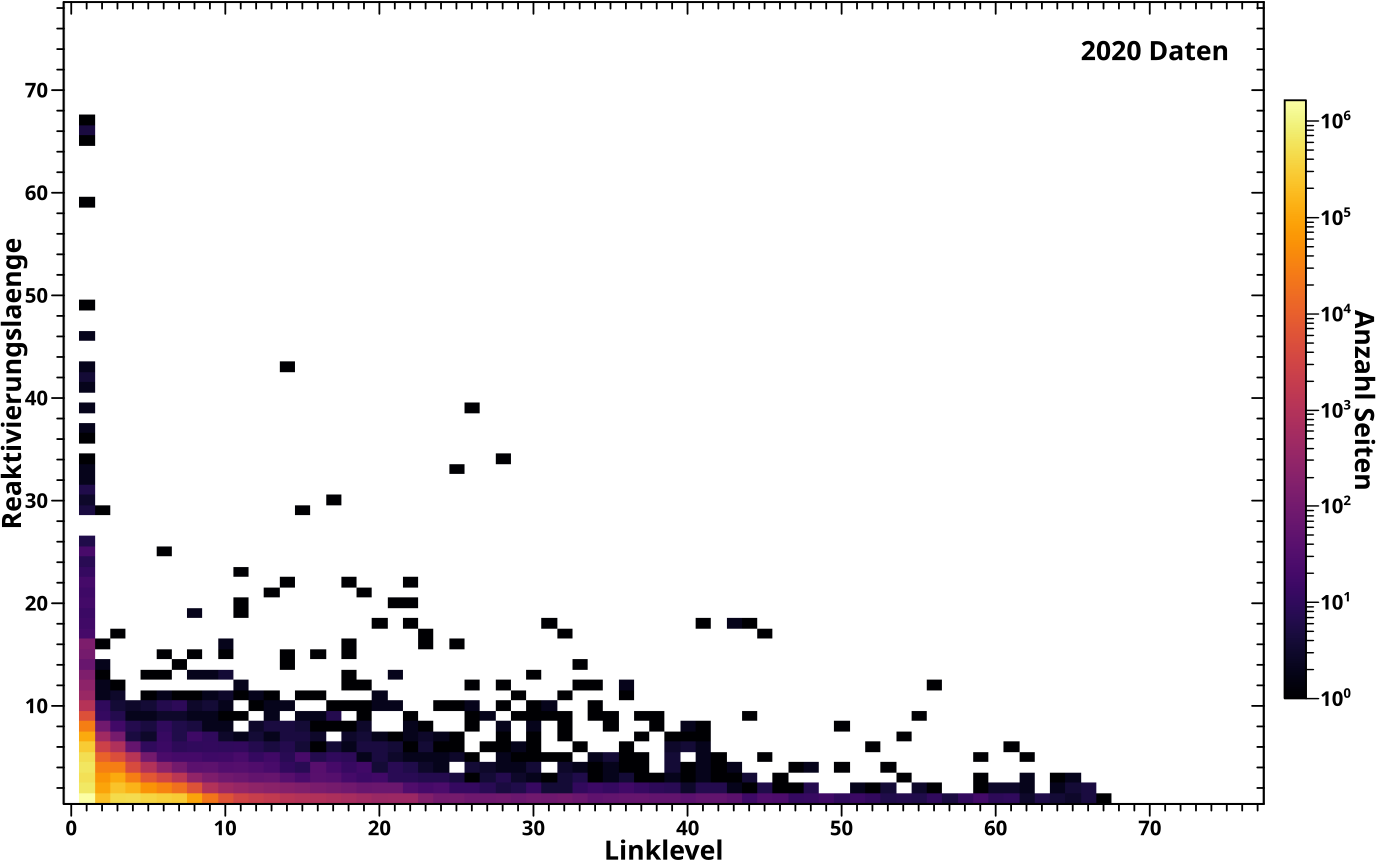
Aber damit war es noch nicht genug, denn die bunten Bilder sind (wie so oft) (Pseudo) 3D-„Karten“ … oder anders: Ich untersuchte eigentlich vielmehr die Haeufigkeit der Reaktivierungslaenge in Abhaengigkeit vom Linklevel … oder noch anders: ich erstellte fuer jedes Linkevel ein Histogramm der Reaktivierungslaengen. Damit ist hoffentlich (wieder) klar, was hier zu sehen ist:

Der wichtigste Unterschied zum damaligen bunten Bild (abgesehen davon, dass ich jetzt eine bessere Farbpalette benutze) ist, dass ich jetzt richtig an die Sache heran gehe. Deswegen sieht man jetzt auch bei LL₁ was (waehrend ich das damals einfach abgeschnitten hatte, denn da war ja nix).

Ansonsten wuerde ich sagen, dass das im Groszen und Ganzen erfolgreich reproduziert ist. Im Detail wuerde ich aber sagen, dass in den 2023 Daten zwei Dinge anders sind. Es scheint weniger lange Reaktivierungslaengen zu geben. Das bezieht sich sowohl auf die Ordinate, als auch auf die Abszisse (deswegen zwei (!) Dinge die anders sind). Wobei „lang“ relativ ist, ich meine aber, dass es deutlich weniger dunkle Punkte weg von den helleren Bereichen gibt. Also weiter nach rechts, wenn man es bezogen auf die Ordinate betrachtet, und weiter nach oben, bezogen auf die Abszisse.
Mein Bauchgefuehl sagt mit, dass das ’n echter Effekt ist; weil wir hier aber sowieso schon mit nur wenigen „Ereignissen“ in den 2020 Daten anfangen, ist das vermutlich relativ schwer systematisch zu untersuchen. Allerdings kønnte man sich das mglw. „Ereigniss“ fuer „Ereigniss“ anschauen, denn man hat es ja mit nur sehr wenigen davon zu tun. Ich belasse das an der Stelle so wie’s ist und das das soll mal wer anders machen.

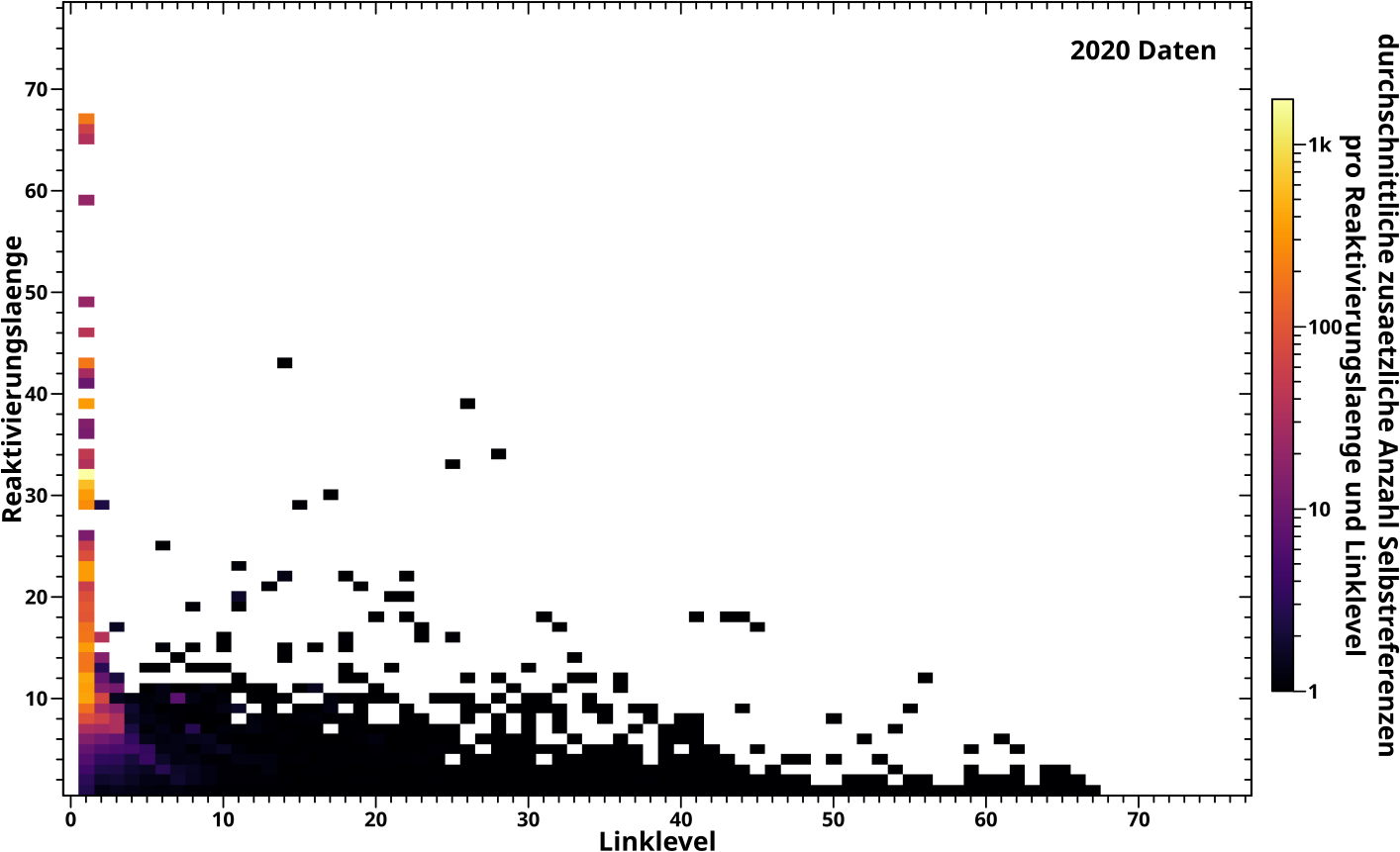
Das zweite bunte Bild damals zeigte die durchschnittlich hinzukommende Anzahl an Selbstreferenzen pro Reaktivierung. Dazu summierte ich zunaechst in jedem Datenpunkt die Summe aller in einer „Reaktivierungskette“ hinzukommenden Selbstreferenzen auf. Ja das ist ’ne doppelte Summe, zunaechst fuer jede Seite die Summer der hinzukommenden Selbstreferenzen (pro Reaktivierung) und dann die Summe ueber alle Seiten die zu einem gegebenen Datenpunkt beitragen. Wenn das fuer alle Seiten getan ist, wird Wert in jedem Datenpunkt durch die Anzahl der Seiten geteilt die beigetragen haben und das Resultat wurde nochmals durch die relevante Reaktivierungslaenge dividiert.

Ein Beispiel macht hoffentlich deutlicher was ich meine. Man denke sich, dass Seite A auf LL₅ reaktiviert wird mit einer Reaktivierungslaenge von drei Linkleveln. Auf LL₅ erhaelt Seite A sieben Selbstreferenzen, auf LL₆ zwei und auf LL₇ eine. Im Datenpunkt (LL₅, Reaktivierungslaenge 3) speichere ich die Summe (7 + 2 + 1 = 10).
Seite B wird nun auch auf LL₅ reaktiviert, aber mit einer Reaktivierungslaenge von nur einem Linklevel und Seite B erhaelt 23 zusaetzliche Selbstreferenzen durch die Reaktivierung. Im Datenpunkt (LL₅, Reaktivierungslaenge 1) speichere ich diesen Werte (23).
Als Letztes dann Seite C, die auch auf LL₅ reaktiviert wird, auch mit einer Reaktivierungslaenge von 3 Linkleveln; Seite C traegt also zum selben Datenpunkt bei wie Seite A. Seite C erhaelt auf LL₅ dreizehn Selbstreferenzen, auf LL₆ sechs und auf LL₇ eine. Im Datenpunkt (LL₅, Reaktivierungslaenge 3) befindet sich bereits die Zahl 10 und dazu wird jetzt die Summe der durch Seite C hinzukommenden Selbstreferenzen (13 + 6 + 1 = 20) addiert. Damit befindet sich danach in diesem Datenpunkt der Wert 10 + 20 = 30.
Das war der erste Schritt (der in Echt natuerlich fuer ca. 6 Millionen Seiten gemacht wurde).

Nun zur Division. Im Datenpunkt (LL₅, Reaktivierungslaenge 3) befindet sich der Wert 30 und der wird zunaechst durch zwei geteilt (weil Seite A und Seite B) beigetragen haben. Das ergibt 15. Diese 15 wird abschlieszend durch die Reaktivierungslaenge (also drei) geteilt. Die durchschnittliche Anzahl an hinzukommenden Selbstreferenzen fuer Seiten die auf LL₅ mit einer Reaktivierungslaenge von drei reaktiviert werden ist somit fuenf.
Zum Wert 23 im Datenpunkt (LL₅, Reaktivierungslaenge 1) hat nur eine Seite beigetragen und weil die Reaktivierungslaenge nur eins ist, ist die Division das Einfachste von der Welt. Oder anders: die durchschnittliche Anzahl an hinzukommenden Selbstreferenzen fuer Seiten die auf LL₅ mit einer Reaktivierungslaenge von eins reaktiviert werden ist dreiundzwanzig.

Im dazugehørigen bunten Bild aenderte sich deswegen „nur“ die Farbe der Punkte und die Bedeutung der Farbskala. Alles andere Dinge (Bedeutung der Abszisse und Ordinate und die Verteilung der Datenpunkte im Bild) blieb gleich.

Ich hatte das damals gemacht, weil ich vermutete, dass bei „hohen“ Reaktivierungen (bezogen sowohl auf das Linklevel, als auch auf die Reaktivierungslaenge … und „hoch“ ist (mit Absicht) relativ „diffus“ gemeint) die durchschnittliche Anzahl an hinzukommenden Selbstreferenzen (pro Reaktivierungslaenge) eins betraegt. Oder anders (an einem Beispiel): wenn eine Seite auf LL₂₃ reaktiviert wird und bis LL₆₅ die Selbstreferenzenkurve nicht wieder abgebrochen wird (das entspricht einer Reaktivierungslaenge von 42), dann vermutete ich, dass das eine zusammenhaenge „Kette“ von 42 Einsen war.

Diese Vermutung wurde damals im Wesentlichen bestaetigt und in den 2023 …

… aendert sich an dem Ergebnis nix.

(Fast) alle Unterschiede zum damaligen bunten Bild kommen durch die selben Mechanismen zustande wie bereits oben diskutiert.

Das „fast“ bezieht sich darauf, dass die Farbskala dieses Mal auch logarithmisch ist (waehrend sie beim letzten Mal linear war). Der Grund liegt in Ausreiszern, also Seiten die viele Selbstreferenzen (und mglw. lange Reaktivierungslaengen) haben, wo aber nur wenige Seiten (mitunter nur eine Einzige) zum Datenpunkt beitragen. Da reduziert die Division den Wert also nicht so stark wie bei den meisten anderen Datenpunkten.
In den 2023 Daten ist das Extrem die Seite „The“ (jup, nix weiter), die auf LL₁ mit einer (re)aktiviert wird, mit einer (Re)aktivierungslaenge von 34 Linkleveln und die dann 374,173 Selbstreferenzen ansammelt. Diesen Wert bringt eine Division durch 34 auch nur runter auf ca. 11-tausend … was natuerlich bei einer linearen Skala alle anderen Punkte in den (dann schwarzen) Hintergrund draengen wuerde.

So … damit ist das Thema „Ausgaenge“ abgeschlossen und ich kann beim naechsten Mal endlich mit den ganz vielen Verteilungen weitermachen.