Søren in Norwegen

Letztes Mal reproduzierte ich die „Aussteiger“. Dabei benutzte ich aber eine etwas andere Herangehensweise als damals. Ich erwaehnte nur kurz, dass die damalige Herangehensweise etwas „haarig“ war in Bezug auf Selbstreferenzen, da die entsprechenden Kurven nicht nur und ausschlieszlich am Ende des (seitenabhaengigen) Linknetzwerks „aussteigen“, sondern das auch schon auf fruehen Linkleveln tun kønnen … um dann u.U. auch wieder „reaktiviert“ zu werden auf nachfolgenden Linkleveln.
Wieauchimmer, da beide Herangehsenweisen zur Ermittling der „Aussteiger“ bei den anderen Grøszen von Interesse zum selben Ergebnis fuehren, und auch das Diagramm der Selbstreferenzen auf den ersten Blick nicht all zu unterschiedlich war, habe ich mich darum zunaechst gar nicht weiter gekuemmert und nur mit …

[d]eswegen sind die roten Balken im linke[n] Diagramm hier nicht identisch zum damaligen Diagramm

… kommentiert.

Natuerlich hat mir das keine Ruhe gelassen, und ich wollte schauen wie grosz die Diskrepanz ist. … … … Und ach du Schreck! … da hab ich ja einen wirklich ernstzunehmenden Fehler gemacht.
Aber der Reihe nach und heute nur mit den 2020 Daten denn hier muss nix in dem Sinne reproduziert werden, denn ich will ja den Fehler diskutieren.

Zur Erinnerung: die neue Herangehensweise findet den „Ausgang“ derart, dass vom Ende einer Kurve, in Richtung Anfang gehend, geschaut wird, bei welchem Linklevel der Wert der Kurve zum ersten Mal UNgleich Null ist. Die damalige Herangehensweise hingegen schaute vom Anfang einer Kurve, in Richtung Ende gehend, bei welchem Linklevel der Wert der Kurve zum ersten Mal GLEICH Null wird.
Wie gesagt, ist das, von den Selbstreferenzen abgesehen, kein Problem, da alle anderen Grøszen von Interesse „durchgehende“ Kurven haben und beide Methoden das selbe Ergebnis liefern. Aber es geht ja um genau diese Selbstreferenzen.

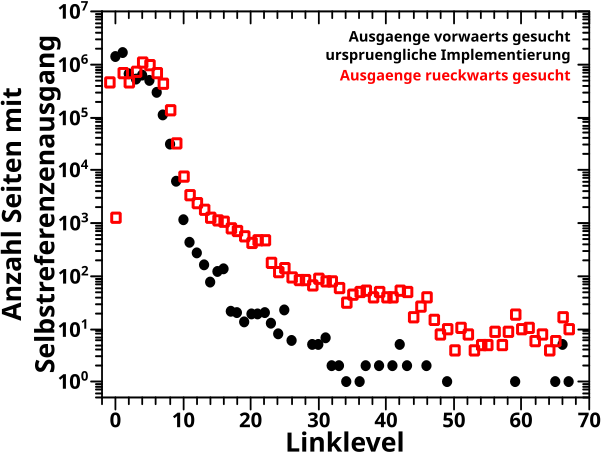
Hier sieht man den Unterschied der Aussteiger-per-Linklevel-Kurven-der-Selbstreferenzen wenn man das wie damals macht (schwarze Punkte, vorwaerts nach der erste Null suchend) bzw. besser (rote Quadrate, rueckwaerts nach dem ersten Wert der ungleich Null ist suchend):

Achtung: Damals hatte ich das Linklevel beim dem zum ersten Mal null Selbstreferenzen auftreten als „Ausgang“ deklariert, waehrend es nach der neuen Methode das Linklevel direkt davor ist was ja noch einen Wert ungleich null hat. Die Punkte von damals wurden dahingehend um ein Linklevel nach Links verschoben; das gilt auch fuer alle folgenden Diagramme.

Das scheint anfangs qualitativ (!) recht gut uebereinzustimmen (davon abgesehen, dass ich damals „flache“ Kurven nicht extra bedacht hatte). Quantitativ gibt’s zwar zum Teil zahlentechnisch grosze Unterschiede die man wg. der logarithmischen Skala (fast) nicht wahr nimmt, das ist aber nicht so wichtig, denn alles was ’n Unterschied von ’nem Faktor weniger als ’ne Grøszenordnung hat ist schon OK.
Was mich zu Werten ueber LL₁₀ bringt; denn ab dort erhaelt man mit der (neuen) Rueckwaertsmethode ca. ’ne Grøszenordnung mehr „Ausgaenge“ als mit der (alten) Vorwaertsmethode.

Aber das ist NICHT der schwerwiegende Fehler, denn das ist erklaerbar mittels „Reaktivierungen“. Es passiert dass eine Kurve die schon „ausgestiegen“ ist, auf einem høheren Linklevel „reaktiviert“ wird. Das ist dann meistens nur das eine einzige Linklevel (oder vllt. auch mal zwei oder drei), auf dem pløtzlich nochmal eine Selbstreferenz auftaucht. Das fuehrt dann natuerlich zu einem weiteren „Ausgang“ (es ist halt nur nicht der erste „Ausgang“ fuer eine gegebene Kurve) der von der Rueckwaertsmethode erkannt wird, wenn es denn der Letzte ist.
Damit die Vorwaertsmethode so weit hinten einen „Ausgang“ registriert, muss die entsprechende Kurve ohne Unterbrechung mindestens eine Selbstreferenz auf jedem Linklevel bis dorthin gehabt haben. Eine so lange ununterbroche Kette von Selbstreferenzen zu haben hat natuerlich eine sehr kleine Wahrscheinlichkeit, weswegen die Vorwaertsmethode bspw. auf LL₃₅ nur einen „Ausgang“ registriert, waehrend die Rueckwaertsmethode 45 „Ausgaenge“ aufspuert (wovon der eine von der Vorwaertsmethode darunter ist).
In anderen Worten: die Diskrepanz hat eine Erklaerung die aus der Natur der unterschiedlichen Methoden kommt, und insb. weil es sich hierbei um eher kleine absolute Zahlen handelt, macht mich der Unterschied nicht wirklich stutzig.

Nun arbeite ich aber an der Reproduzierbarkeit und da ist’s kontraproduktiv die Methode zu aendern (auch wenn es die bessere Methode ist). Das wurmte mich und deswegen setzte ich mich ran und hackte kurz die Vorwaertsmethode zusammen. Weil ich gute Vorarbeit geleistet habe ging das recht fix. … … … Und hier ging der „Aerger“ los.

Alles fing damit an, dass ich mittlerweile von „flachen“ Kurven (also solchen die keine einzige Selbstreferenz haben) gelernt hatte. Damals hatte ich die ueberhaupt nicht beachtet. Nun wollte ich die aber mit unterbringen. Deswegen muss ich nochmal kurz auf die Rueckwaertsmethode zu sprechen kommen und erklaeren warum die der Vorwaertsmethode ueberlegen (und vorzuziehen) ist um die „Ausgaenge“ zu bestimmen.

Es gibt bei der Rueckwaerrtsmethode nur zwei Bedingungen und alles andere folgt zwingend aus denen. Erstens: geh rueckwaerts, Zweitens: der erste Wert ungleich Null ist der Ausgang. Simpler als das geht’s nicht. Und wenn man mal nachdenkt ist die erste Bedingung keine richtige Bedingung denn man kann eine Dynamik nicht erforschen, wenn man sich nicht bewegt; man braucht also zwingend eine „Bewegungsrichtung“. Wichtig ist nur zu wissen, wann man stoppen muss (wann man also das gefunden hat wonach man sucht). Ich sage jetzt also mal, dass es nur EINE Bedingung gibt … einfacher geht’s nicht.
Man sieht leicht, dass da automatisch der „wahre Ausgang“ rausfaellt, denn bei der Rueckwaertsmethode muss man sich nicht drum kuemmern ob eine Kurve mehrere vorherige „Ausgaenge“ hat und dann nochmal „reaktiviert“ wird. Auszerdem folgt automatisch dass eine Kurve flach ist wenn man bis LL₀ kommt und kein einziger Wert ueber Null liegt.

Nun zurueck zur Vorwaertsmethode; im Namen liegt bereits die „Bewegungsrichtung“, womit das gegessen ist. Oben schrieb ich, dass ich schaute, wann der erste Wert Null wird als „Ausgangsbedingung“. Das alleine ist zunaechst eine genauso simple Regel aehnlich bei der Rueckwaertsmethode. Die ist aber leider nur notwendig und nicht hinreichend. Insb. dann wenn man flache Kurven unterscheiden will, denn bei denen liegt ja bereits auf LL₀ der Wert Null vor … ich kann aber nicht entscheiden ob eine Kurve flach ist, ohne durch alle Linklevel durchgegangen zu sein.
Deswegen muss man eine zweite Bedingung anfuehren und die Erste etwas modifizieren: ein „Ausgang“ liegt vor, wenn der Wert auf einem gegebenen Linklevel UNgleich Null und der Wert auf dem naechsten (!) Linklevel GLEICH Null ist. Kommt man am Ende aller Linklevel an und beide Bedinungen lagen nie gleichzeitig vor, hat man (automatisch) eine flache Kurve (fuer die die „gleich Null“ Bedingung ueberall gilt).

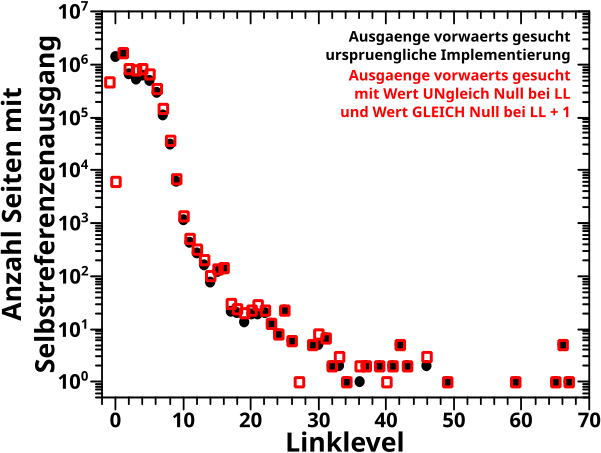
Damit erhaelt man dieses Diagramm:

Das sieht auf den ersten Blick ganz gut aus. Es gibt ein rotes Quadrat bei LL_{minus 1} fuer die flachen Kurven und deswegen stimmen die Werte bei LL₀ nicht ueberein (denn frueher hatte ich beides in LL₀ zusammengefasst). Das ist also OK … Aber Moment mal! Wieso findet die neue Vorwaertsmethode einen Wert bei LL₂₇ (und ein paar anderen Linkleveln) die alte aber nicht? Und ueberhaupt scheinen die schwarzen Punkte und Quadrate etwas gegeneinander verschoben zu sein! (Das sieht man bei linearer Ordinate deutlich deutlicher). Beides sollte nicht vorkommen, ich muss hier also was „falsch“ machen … Hinweis: ich habe damals was (maechtig) falsch gemacht.

Also suchte ich nach dem alten Code … und konnte den nicht finden. Ich bin mir ziemlich sicher, dass der irgendwo ist, aber der alte Code ist so ein Saustall (was ja die Motivation fuer den Reproduktionsteil des ganzen Projekts ist, weil ich eben auch den Code ordentlich machen wollte, damit ich das publizieren kann), dass ich den entsprechenden Teil nicht mittels Schlagwortsuche gefunden hab und ich wollte nicht durch mehrere tausend Linien Code lesen. Auszerdem gibt es eine gewisse Wahrscheinlichkeit, dass ich den tatsaechlich geløscht habe … das liegt an einer gewissen Eigenheit meines Modus Operandi, aber da geh ich jetzt nicht naeher drauf ein.

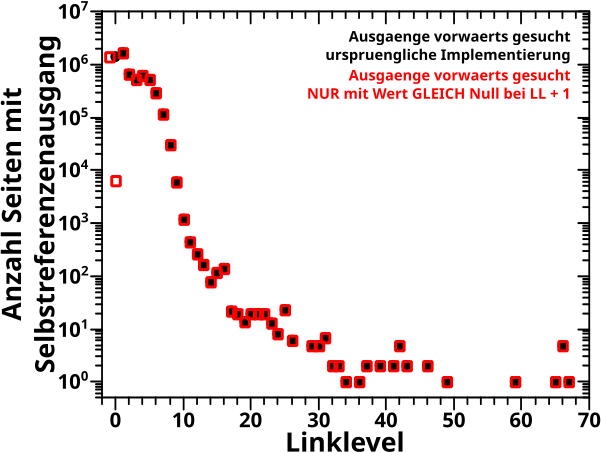
Also ueberlegte ich was ich damals gemacht haben kønnte und zum Glueck war mein (neuer) Code jetzt „gut sortiert“ und mittels nur einer winzigen Aenderung konnte ich die „Wert auf einem gegebenen Linklevel muss UNgleich Null“-Bedingung rausschmeiszen … denn an die hatte ich damals ja gar nicht gedacht. Es bleibt also nur „Wert auf dem naechsten Linklevel muss GLEICH Null sein“ uebrig. Und siehe da …

… das passt … Hurra! Also auszer von den Werten bei LL_{minus 1} und LL₀ abgesehen, aber die stimmen in der Summe mit dem alten Wert bei LL₀ ueberein. Super! Reproduziert … … … … … … … … … aber hmmmm … hier stimmt doch was nicht! … … … Der Beitrag ist nur jetzt schon so lang, sodass ich den Rest der Diskussion auf’s naechste Mal verschiebe.