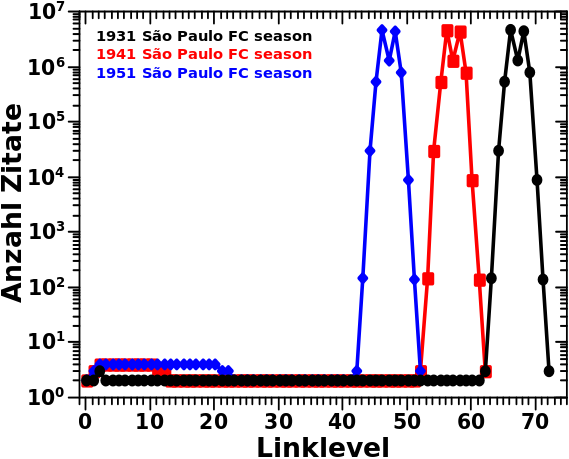
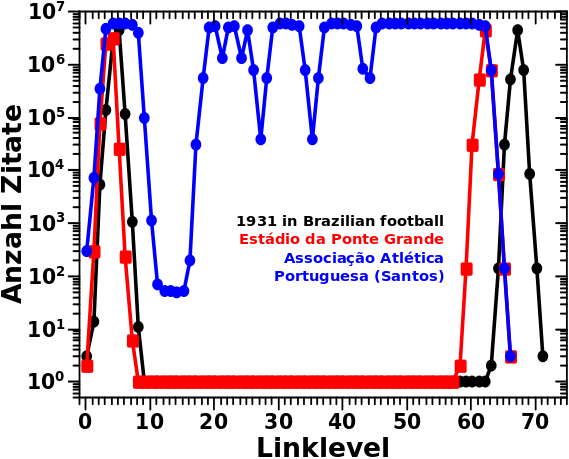
Beim letzten Mal hatte ich gezeigt wie die Verteilungen der Linkfrequenzen fuer drei Seiten des „São Paulo FC“-Artefakts aussehen. Zur Erinnerung: diese weisen ein zweigeteiltes Maximum auf (das zweite Maximum ist etwas kleiner) welche durch ein Phaenomen das ich „Reflexion“ nannte (und dort genauer beschrieb) zustande kommt.
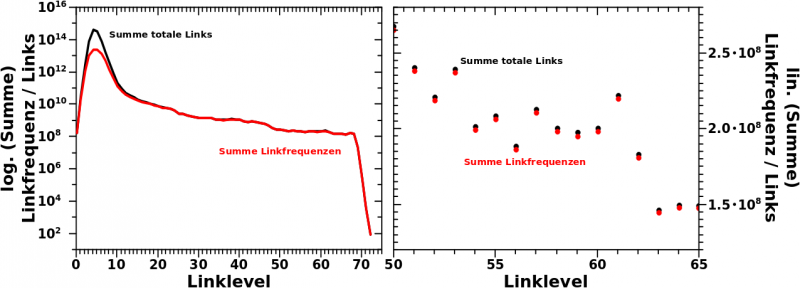
Nicht zu vergessen ist, dass ich das Mysterium aufklaeren will, warum die Anzahl der totalen Links und die Anzahl aufsummierten Linkfrequenzen so nahe beieinander liegen fuer høhere und hohe Linklevel. Aber eben _weil_ die so nahe zusammen liegen muss ich genau wissen, wie die Werte fuer die Grøszen zustande kommen; daher der Titel dieses Beitrags.
All das Zaehlen veranschauliche ich genau anhand eines Beispiels: welche Seiten tragen auf LL66 zur Linkfrequenz bei; dito bzgl. der totalen Links. Am Ende diskutiere ich dann, inwieweit das verallgemeinert werden kann.
Also auf geht’s mit allen (!) Seiten die auf LL66 von anderen Seiten zitiert werden.
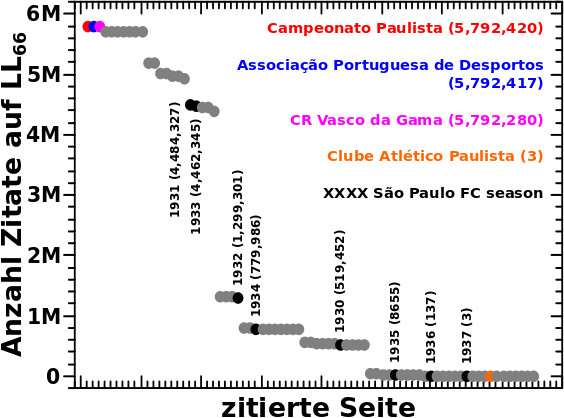
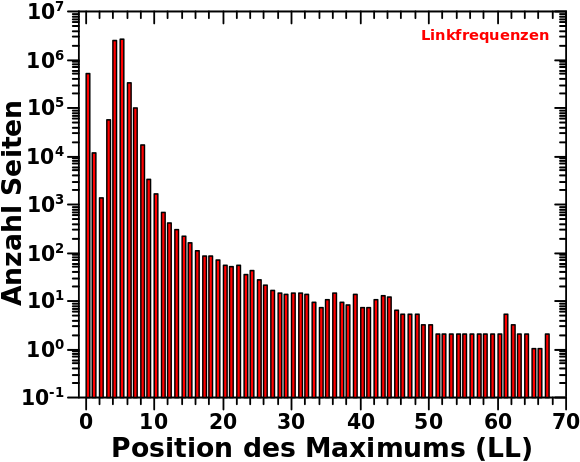
Nur 75 Seiten werden ueberhaupt auf LL66 zitiert. Und alle davon erhalten Zitate NUR von den Jahren 1936 bis 1930 des „São Paulo FC“-Artefakts. Weiter unten wird klar warum das so sein muss. Farbig hervorgehoben sind ein paar Beispiele und wie viele Zitate diese auf LL66 erhalten sind angegeben. Diese Werte sollen nun erklaert werden. Aber dazu muss ich etwas weiter ausholen und zunaechst nochmal ein Ergebnis von vor langer Zeit zeigen (ich bitte zu entschuldigen, dass ich hier uneinheitlich bin und Punkte, anstatt Kommas (wie oben), als Trennung nach jeder dritten Stelle benutz(t)e):
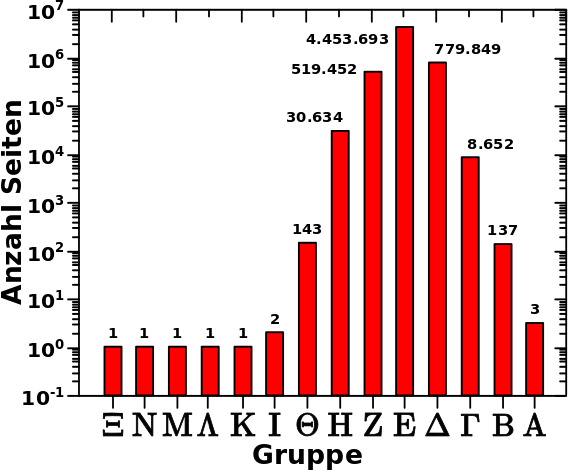
Zur Erinnerung: das ist nur ein Hereinzoomen in das Ende der Verteilung der Aussteiger (bezogen auf die totalen Links) pro Linklevel. Das bedeutet je weiter links ein Balken liegt, umso eher ist der „ausgestiegen“. Im hiesigen Zusammenhang bedeutet das, dass die Seiten die einen weiter links liegenden Balken ausmachen, ein gegebenes Jahr des Artefakts frueher durchlaufen haben und sich damit schon im darauffolgenden Jahr befinden. Die Gruppennamen sind heute im Wesentlichen nicht zu beachten; nur die Zahlen an den Balken sind wichtig (und das was ich im Satz zuvor schrieb).
Das Diagramm ganz oben zeigt, dass die 1931 São Paulo FC season auf LL66 am meisten zitiert wird und dort 4,484,327 Zitate hat. Aus der ersten Untersuchung des Artefakts wissen wir auch, dass die Seiten das Selbige schøn der Reihe nach, von hohen zu niedrigeren Jahren, durchlaufen. Daraus folgt dann, dass sich die meisten Seiten im Jahre 1932 des Artefakts befinden und von dort 1931 zitieren.
Aus dem zweiten Diagramm lesen wir nun ab, dass „die meisten Seiten“ bedeutet, dass es sich dabei um 4,453,693 handelt. Das reicht nicht ganz fuer die Anzahl der Zitate die 1931 erhaelt. Hier kommt aber die „Reflexion“ ins Spiel, denn wie erwaehnt sind die Seiten die den Balkens der zwei Schritte weiter links liegt ausmachen bereits im Jahre 1930. Von dort wird 1931 natuerlich auch zitiert.
Schwuppdiwupp: 4,453,693 + 30,643 = 4,484,327 … fetzt, wa!
Das erklaert ebenso, warum das Jahr 1933 mit 4,462,345 die zweitmeisten Zitate erhaelt. Das sind zunaechst wieder die 4,453,693 Seiten auf 1932 die zurueck nach 1933 reflektieren. Und dann noch die 8,652 „Nachzuegler“ die sich auf LL66 erst im Jahre 1934 befinden und von dort 1933 zitieren.
So kann man das mit allen Seiten des Artefakts machen. Dabei sieht man dann, dass sich auf LL66 keine einzige Seite in spaeteren Jahren (also somit frueher in der „Artefaktkette“) sein kann als 1936. Denn das sind die letzten drei Nachzuegler die sich dort befinden, alle spaeteren Jahre wurden bereits von allen Seiten komplett durchlaufen.
Soweit dazu. Wie erhaelt nun aber die Campeonato Paulista 5,792,420 Zitate?
Ganz einfach, die wird in allen Jahren die auf LL66 noch „aktiv“ sind (also von 1936 bis 1930) zitiert. Wenn man die Summe der Zahlen bildet die an den letzten sieben Balken stehen, dann kommt man auf genau diese Zahl.
So macht man das auch fuer den Associação Portuguesa de Desportos muss aber beachten, dass dieser im Jahre 1936 NICHT zitiert wird. In 1936 befinden sich ja nur noch die letzten 3 Nachzuegler, somit fehlen drei Zitate (wie angegeben).
Der CR Vasco da Gama wird nicht zitiert in den Jahren 1936 und 1935. Deswegen muessen von der maximalen Anzahl an møglichen Zitaten welche die Campeonato Paulista erhalten hat 3 + 137 (die letzten zwei Balken) abgezogen werden.
Und das geht dann so weiter, bis man beim Clube Atlético Paulista (und allen anderen Seiten die nur drei Zitate erhalten) ankommt, denn diese werden nur noch im Jahre 1936 zitiert.
Super. Damit ist der Ursprung der Zitate aufgeklaert und die Summe ueber alle Punkte des obersten Diagramms ergibt, dass die Summe aller Linkfrequenzen auf LL66 133,684,373 betraegt.
Ich muss eingestehen, dass ich peinlich lange brauchte um all das genau heraus zu bekommen und zu verstehen woran das liegt. Denn der Ansatz den ich oben schrieb der kam mir erst beim Zusammenschreiben. Ich naeherte mich der Sache auf eine kompliziertere Art und Weise wo ich genau aufpassen musste von wo welche Seite zitiert wird und in welchen Jahren sich jetzt die zitierenden Seiten (und wie viele von denen) genau befinden und wie sich das durchzieht. Das Verstehen hat mir natuerlich geholfen das relativ kurz und knapp oben zusammen zu fassen und den Zusammenhang zu einem frueheren Ergebis zu sehen und warum das richtig ist das so zu machen anstatt des urspruenglichen, komplizierteren Ansatzes.
Wieauchimmer, nun zur Anzahl der totalen Links; nach obigem Erbsenzaehlen ist das beinahe trivial.
Wir wissen, dass sich alle Seiten nur noch in den Jahren 1936 bis 1930 befinden. Getreu dem Titel dieses Beitrags heiszt das ganz konkret:
– 30,634 Fruehaufsteher sind auf LL66 bereits im Jahr 1930 mit 27 Links,
– 519,452 Fruehaufsteher sind auf LL66 bereits im Jahr 1931 mit 30 Links,
– die 4,453,693 Seiten des Hauptfelds sind auf LL66 im Jahr 1932 mit 22 Links,
– 779,849 Nachzuegler sind auf LL66 noch im Jahr 1933 mit 26 Links,
– 8,652 Nachzuegler sind auf LL66 noch im Jahr 1934 mit (ebenso) 26 Links,
– 137 Nachzuegler sind auf LL66 noch im Jahr 1935 mit 24 Links und endlich
– 3 Nachzuegler sind auf LL66 noch im Jahr 1936 mit 31 Links.
Wenn man die Gruppengrøsze mit der Anzahl der Links multipliziert und dann alles aufsummiert, erhaelt man genau 134,896,331 totale Links auf LL66.
Damit ist das Mysterium auch aufegklaert, denn grob gesagt _muessen_ die Summen ueber diese zwei Grøszen (totale Links und Linkfrequenz) per Linklevel so nahe beieinander liegen. So viele verschiedene Links wie man hat ungefaehr genau so viele Zitate (Linkfrequenz) erhaelt man. Aber Letztere sollten immer ein bisschen darunter liegen.
Zur Veranschaulichung stelle man sich zunaechst vor, dass _alle_ Seiten des Artefakts von 1936 bis 1930 genau 23 Links haben und zwar die 23 selben (!) Links. Dann liegt fue jede dieser verlinkten Seiten eine Situation wie bei Campeonato Paulista vor und die wuerden alle maximal viele Zitate auf LL66 haben; naemlich 5,792,420. Die Summe ueber alle diese Linkfrequenzen ergaebe 133,225,660.
Wenn nun aber jede dieser Seiten 23 Links hat, dann folgt nach der zweiten detaillierten Rechnung oben, dass man auch genau so viele totale Links hat.
Nun stelle man sich vor, dass ein (und nur ein) Link mit einem anderen Link ausgetauscht wird. Die Anzahl der total Links bleibt in dem Szenario gleich. Der ausgetauschte Link (bzw. die Seite auf die der verweist) erhaelt nun nicht mehr die maximale Anzahl an Zitierungen. Vielmehr sind es nur noch so viele Zitate, wie sich Mitglieder in der Gruppe befinden, die sich auf dem gegebenen Linklevel auch auf der Seite mit besagtem ausgetauschtem Link aufhalten. Das ist im Wesentlichen das was oben bei allen anderen Seiten passierte die nicht Campeonato Paulista sind.
Und deswegen muss die Summe ueber die Linkfrequenzen zwar nahe an der Summe der totalen Links sein, kann aber maximal gleich grosz werden und ist aufgrund der geschilderten Ursache aber in allen Faellen kleiner.
Damit hat sich das Mysterium so’n kleines bisschen umgekehrt und die Frage ist nun, warum es bei kleinen Linkleveln Grøszenordnungen kleiner ist? Das ist schnell erklaert und liegt (wieder) an der Zaehlweise der Linkfrequenz.
Auf kleinen Linkleveln hat eine Ursprungsseite „Zugriff“ auf URST viele Seiten (einfach, weil sich das Linknetzwerk so schnell verzweigt). Dadurch hat man auch eine entsrpechend hohe Zahl an (totalen) Links und je nach Linklevel sind dies hauptsaechlich Mehrfachzaehlungen. Das natuerlich deswegen, weil Seiten oft von mehreren (anderen) Seiten zitiert werden und von Letzteren kønnen sich mehrere auf dem selben Linklevel wiederfinden (einfach weil es da so viele Seiten gibt).
Bei der Linkfrequenz wird aber jede zitierte Seite nur ein Mal pro Linklevel gezaehlt, egal wie viele Zitate die wirklich erhaelt. Und das fuehrt bei kleinen Linkleveln zu einer hohen Diskrepanz.
So, nun ist’s aber genug mit der Erbsenzaehlerei. Mal schauen, was ich beim naechsten Mal mache.