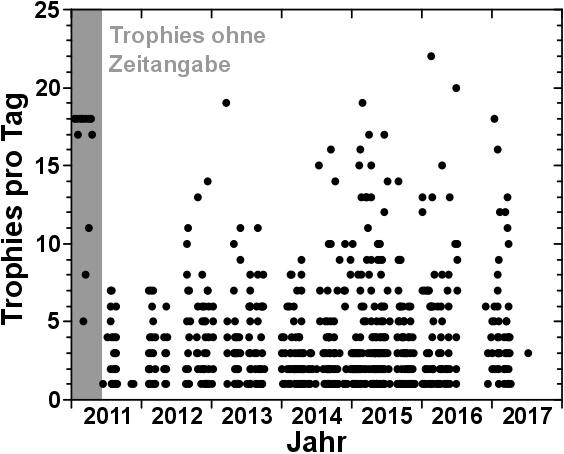
Im ersten Teil zeigte ich euch, meinen lieben Leserinnen und Lesern, wie viele Trophies ich pro Tag erhielt, ueber alle Jahre die ich meine Playstation 3 bereits habe.
SO …
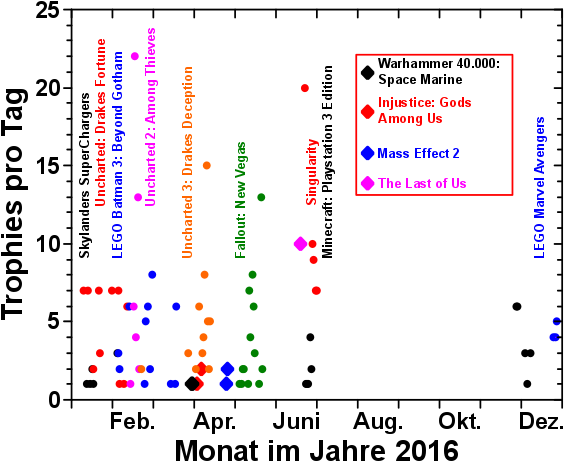
… sieht mein typisches Spielverhalten in einem Jahr aus.
Um Weihnachten/Neujahr rum werden “kinderfreundliche” *hust* Spiele gespielt (2016 waren das Skylanders SuperChargers und LEGO Marvel Avengers), waehrend ich nur fuer mich natuerlich auch was zocke (Uncharted: Drakes Fortune in diesem Fall).
Ueber das Jahr verteilen sich dann so einige weitere Stunden des Zockens mit dem jungen Mann der bei mir wohnt und ich zocke auch mehr fuer mich selber.
Ab und zu habe ich mal keine Lust zu zocken oder bin durch Urlaub daran gehindert. Dies aeuszert sich durch kuerzere oder laengere Pausen, in denen ich dann auch keine Trophies bekomme. 2016 war eine solche Pause ungewøhnlich lang, von Anfang Juli bis Ende November.
Im Allgemeinen beende ich ein Spiel, bevor ich ein Neues anfange.
Aber manche Trophies dauern laenger, bis ich die habe. Meist im Zusammenhang mit online-Spielen, denn mir fehlen da einfach die “Skills” sodass es etwas laenger dauert. Oder aber, weil die Bedingungen fuer gewisse Trophies derart sind, dass ich echt ewig brauche, bis diese erfuellt sind. Oder weil ein Add-On (oder DLC wie das heutzutage heiszt), eine Weile braucht bevor es erscheint.
In diesen Faellen habe ich dann das Hauptspiel (lange) vorher beendet, aber ueber die Jahre poppen dann noch hier und da ein paar Trophies auf. Diese Faelle sind durch die dicken Diamanten in der obigen Abbildung gekennzeichnet.
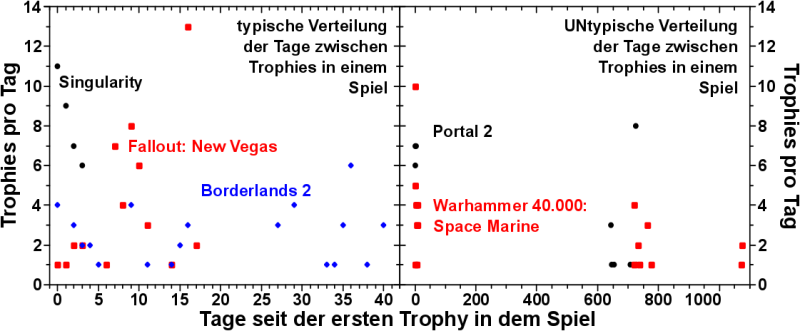
Dieses “typische” und “un-typische” Erhalten von Trophies kann ich dadurch visualisieren, indem ich fuer ein Spiel darstelle, wie viele Tage vergangen sind, zwischen der ersten Trophy in einem Spiel und den jeweils Nachkommenden.
Manche Spiele zocke ich an wenigen Tagen durch (bspw. Singularity, ein Spiel, welches ich im Uebrigen absolut empfehle).
Fuer komplexere Spiele (wie zum Beispiel Fallout: New Vegas) brauche ich ueblicherweise so ca. zwei bis drei Wochen.
Wenn ich ein Spiel mit dem jungen Mann der bei mir wohnt zusammen zocke (in diesem Fall Borderlands 2 … bei Interesse erklaere ich in persønlichen Gespraechen, warum ich dieses spezifische Spiel mit dem jungen Mann, der bei mir wohnt, gezockt habe), dann wird das natuerlich unterbrochen durch die Zeit, die er leider nicht bei mir wohnt und der ganze Trophy-Fortschritt zieht sich etwas in die Laenge.
Im rechten Bild sieht man dann die oben erwaehnten untypischen Faelle.
Portal 2 (ZOCKEN!!!) zockte ich zunaechst allein. Es dauerte ca. 2 Jahre, bevor der kleine Mann mich besuchte und ich endlich die Co-Op Kurse spielen konnte und somit noch mehr Trophies erhielt.
Warhammer 40k: Space Marine spielte ich, bevor ich online-Aktivitaeten weniger dogmatisch gegenueber stand.
Als ich es dann aber endlich ueber mich brachte mein Spielverhalten direkter zu offenbaren, machte ich mich, 719 Tage nachdem ich die erste Trophy in diesem Spiel erhielt, auf die Jagd, nach noch mehr Trophies. Fuer die allerletzte Trophy musst ich dann noch ziemlich genau ein weiteres Jahr mit jemanden aus Nordirland grinden bevor ich die erhielt. Dabei handelt es sich aber auch um eine Trophy die nur 1,73 % aller Spieler welche dieses Spiel besitzen, erhalten haben. Auf dieses Durchhaltevermøgen bin ich ein klein wenig stolz :) .
Ein letzter untypischer Fall sind Spiele, wo zwischen der ersten und der letzten Trophy null oder nur ein Tag(e) liegen. Rocksmith ist so ein Spiel. Das zaehlt aber nicht, denn das spielte ich mal eine kurze Weile und merkte dann, dass eine echte Gitarre ein Instrument ist, welches mir einfach nicht liegt.
Ein besseres Beispiel ist Terminator: Salvation.
Das war so kurz und einfach, dass da mal ein Power-Gaming-Nachmittag fuer ausreichte, um eine der (fuer Nerds) schønsten Platintrophies zu bekommen.
Genug fuer heute.