Beim letzten Mal schrieb ich ueber die (eher zufaellige) Entdeckung der versteckten Eleganz des Universums in Muenzwuerfen.
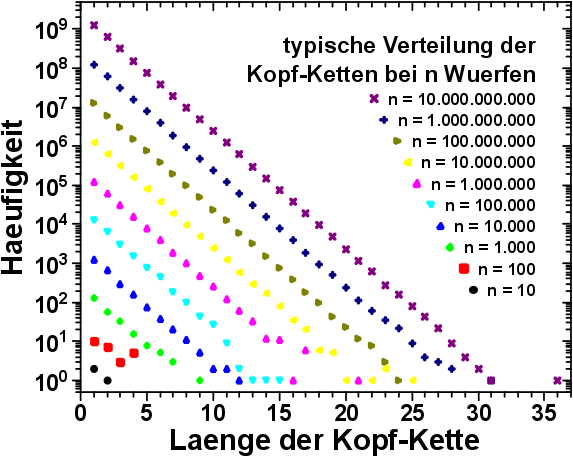
Dies konnte ich natuerlich nicht einfach so auf sich belassen und schaute mir mal an, wie das bei Experimenten unterschiedlicher Laenge aussieht:
Die Verteilungen der Kopf-Ketten bei unterschiedlich lang dauernden Experimenten sind parallel zueinander. Da muss also mehr dahinter stecken.
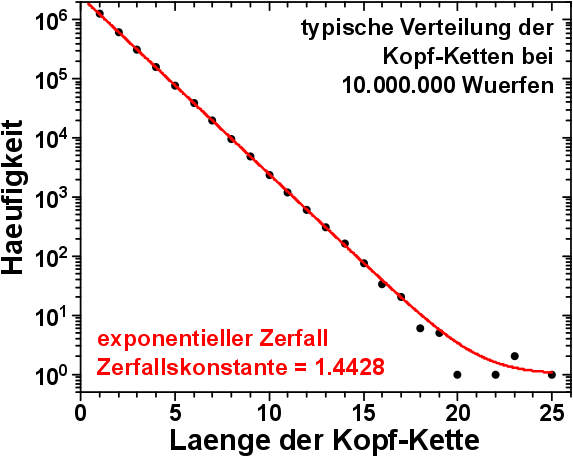
Wenn bei logarithmischer Darstellung Geraden zu sehen sind, dann faellt mir als Physiker natuerlich erstmal ein, diese mittels einer exponentiellen Funktion zu modellieren. In diesem Fall waere es natuerlich ein exponentieller Zerfall und das sieht so aus:
Das Reziproke der Zerfallskonstante ist 0,6931. Und das war mir verdaechtig nahe dem Wert der Standardabweichung der Normalverteilung.
Also dachte ich, dass da mehr dahinter steckt. Dass møglichwerweise in der Zerfallskonstante irgendwie die angenommene Wahrscheinlichkeitsverteilung liegt.
Das war so nicht ganz richtig, aber auch nicht vøllig daneben. Zu Letzterem aber mehr in einem spaeteren Beitrag. An dieser Stelle sei nur so viel gesagt, dass ich ein paar Ueberlegungen anstellte und noch mehr Experimente machte, dies mich aber dem Geheimnis hinter dem Wert der Zerfallskonstante nicht naeher brachte.
Also fasste ich allen Mut zusammen und sprach mal mit einem Mathematikexperten darueber. Zufaelligerweise .oO(Wortspielkasse!) war gleich der erste Experte mit dem ich sprach, Øyvind Bakke, ein Professor der sich professionel mit Statistik beschaeftigte.
Als ich mein Problem beschrieb, hatte er nicht gleich die Løsung parat. Aber die trudelte wenig spaeter per elektronischer Post ein.
Natuerlich ist das, mit dem ich hier auf meinem niedriegen Niveau spiele, schon lange erforscht. Und die vermutete Eleganz ist tatsaechlich vorhanden. Aber dafuer muss ich etwas weiter ausholen und leider (?) zum ersten Mal in diesem Weblog mit Formeln arbeiten.
Traditionellerweise wird die Wahrscheinlichkeit, mit der ein Ergebniss eintritt als \(p\) bezeichnet. Das steht møglicherweise fuer „probability“. Die Wahrscheinlichkeit, dass ein Ereignis eintritt, kann niemals grøszer sein als 100%.
Wenn mehrere Ereignisse eintreten kønnen, so ist die Summe aller Wahrscheinlichkeiten 100%. Da man immer das Resultat „es passiert nichts“ mit einbeziehen muss, ist also garantiert, dass immer irgendwas passiert … Tihihihi.
Bei einem Muenzwurf kønnen nur zwei Ereignisse eintreten. Die Wahrscheinlichkeit fuer „Zahl“ sei mit \(p\) bezeichnet. Die Wahrscheinlichkeit fuer „Kopf“ ist dann natuerlich 100% minus die Wahrscheinlichkeit fuer Zahl. Da 100% gleich 1 (eins) ist, kann man dies schick schreiben als \((1-p)\).
Im Fall einer fairen Muenze ist diese Wahrscheinlichkeit \(p\) natuerlich 1/2, aber ich møchte zunaechst auf dieser etwas abstrakten Ebene verbleiben.
Wenn Kopf liegt, dann betraegt die Wahrscheinlichkeit Zahl im naechsten Wurf zu bekommen: \(p\).
Wenn Kopf liegt, dann betraegt die Wahrscheinlichkeit nochmals Kopf im naechsten Wurf zu bekommen: \((1-p)\).
Die Wahrscheinlichkeit, dass man, wenn Kopf bereits liegt, bei zwei weiteren Wuerfen Kopf und dann Zahl bekommt ist also: \((1-p)\cdot p\). Dies ist die Wahrscheinlichkeit fuer eine Kopf-Kette der Laenge 2. Nicht vergessen, es lag bereits Kopf und wir haben dazu noch zwei Wuerfe dazu genommen und im letzten Wurf wurde die Kette mit Zahl abgebrochen.
Die Wahrscheinlichkeit, dass man, wenn Kopf bereits liegt, bei drei weiteren Wuerfen Kopf, nochmals Kopf und dann Zahl bekommt ist: \((1-p)\cdot (1-p) \cdot p\). Dies ist die Wahrscheinlichkeit fuer eine Kopf-Kette der Laenge 3.
Dies setzt sich weiter fort und die Wahrscheinlichkeit eine Kopf-Kette der Laenge \(n\) zu erhalten ist somit: \((1-p)^{(n-1)}\cdot p\).
Dies ist eine sogenannte geometrische Verteilung.
Meine empirischen Experimente kann man nun interpretieren als Frequenz \(f\), wie oft eine Kopf-Kette der Laenge \(n\) auftritt.
Da ich die Frequenz logarithmisch aufgetragen (und wichtiger mittels eines exponentiellen Zerfalls modelliert) habe erhalte ich also:
\(\ln f = \ln \left[ (1-p)^{(n-1)} \cdot p\right] = (n-1) \cdot \ln(1-p) + \ln p\).
Um die Abbildung und insbesondere den Verlauf der roten Kurve zu beschreiben, muss man im Hinterkopf haben, dass in diesem Falle \(n\) das Argument und \(f\) der Funktionswert ist.
Benutzen wir nun ganz konkret 1/2 als die Wahrscheinlichkeit Zahl zu werfen ein, so erklaert sich der Wert fuer den „Abfall“ der Modellierungskurve – die Zerfallskonstante (oder vielmehr das Reziproke der Zerfallskonstante). Der Logarithmus naturalis von 2 ist naemlich ungefaehr 0,6931.
Warum ich jetzt das Reziproke der Zerfallskonstante betrachtet habe, haengt damit zusammen, wie man den exponentiellen Zerfall definiert. Oft wird dieser naemlich mit einem Bruch im Exponenten geschrieben und wenn man den nicht haben will, nimmt man einfach den reziproken Wert. Aber ich verliere mich hier gerade etwas in Details.
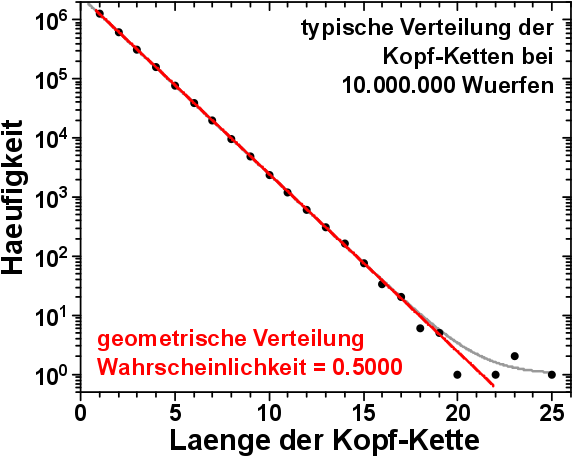
Passen wir nun den im vorherigen Bild gezeigten Datensatz mit dem richtigen Modell an, so erhalten wir:
YEAH!!! Das passt ja super!
Die graue Kurve ist der bereits oben besprochene exponentielle Zerfall, denn ich finde es schon interessant, wie sich zwei vøllig verschiedene Modelle (und damit Implikationen) der Realitaet doch ziemlich gut annaehern. Das ist so wie der Unterschied zwischen den Gravitationstheorien von Newton und Einstein. Beides sind nur Modelle und Newton ist definitiv mehr falsch als Einstein. Aber wenn ich mich nur in Bereichen bewege, in denen das nicht relevant ist, muss ich mich nicht mit der komplizierteren Sache herumschlagen. Toll wa!
Nun da die Neugier, wo die Eleganz des Universums herkommt, befriedigt ist, komme ich zurueck zum eigentlichen Thema: „Wie unfair ist eine Muenze zu mir, wenn ich diese werfe?“
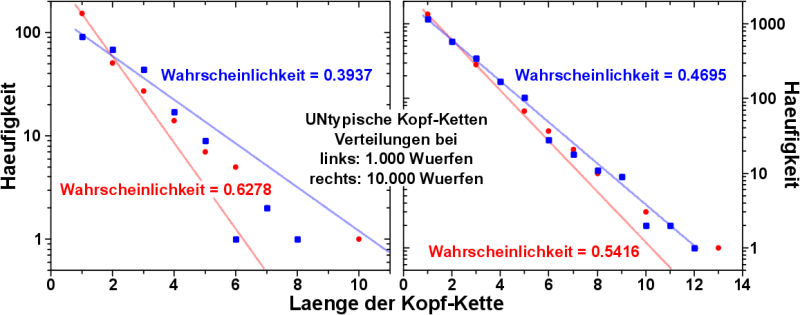
Dies ist in diesem Bild veranschaulicht:
Hier sind untypische Kopf-Ketten Verteilungen fuer jeweils zwei Experimente (aus jeweils 1.000) mit jeweils 1.000 bzw. 10.000 Wuerfen dargestellt. Denn 1.000 Mal eine Muenze werfen ist durchaus etwas, was man machen kann. Da braucht man nur eine Klasse mit 10 Schuelern und laeszt die 100 Mal ’ne Muenze werfen. Bzw. macht man das 10 Jahre lang, dann hat man 10.000 Muenzweurfe.
Passt man die Ergebnisse mittels der geometrischen Verteilung an, um den Wahrscheinlichkeitswert fuer Zahl heraus zu bekommen, so kønnen sich diese Werte massiv voneinander unterscheiden. Ich muss zugeben, dass die hier gezeigten Werte nicht nur untypisch, sondern extrem waren, suchte ich doch extra die grøszten / kleinsten Wahrscheinlichkeitswerte unter all den jeweils 1.000 Experimenten heraus.
Die extremen Wahrscheinlichkeitswerte fuer die Daten im linken Graphen bedeuten, dass selbst bei 1.000 Wuerfen mit einer eigentlich fairen Muenze, die Schwankungen so extrem sein kønnen, dass es aussieht, dass die Muenze NICHT fair ist, sondern eine (erhebliche!) Tendenz zu einem der beiden Resultate hat. Und dabei denkt man doch landlaeufig (also zumindest ich dachte das bisher), dass 1.000 Wuerfe schon ’ne gute Statistik sind.
An den Wahrscheinlichkeitswerten im rechten Graphen sieht man aber auch, dass die extremen Werte weiter zusammen ruecken. Untypische Kopf-Ketten Verteilungen werden also immer typischer. Im Falle des 1.000-mal-10-Millionen-Wuerfe-Experiments betrug die Diskrepanz zwischen den beiden extremsten Wahrscheinlichkeitswerten uebrigens nur noch ca. 0,0021.
Aber 10 Millionen Wuerfe. Da braucht man schon die Schueler eines ganzen Landes fuer um das zu realisieren … .oO(MUAHAHAHAHAHA).
Leave a Reply