Søren in Norwegen

Im Zuge der Ueberlegungen zu dieser Serie ist mir meine Tante Anneliese (eigentlich die Schwester meiner Oma) eingefallen. Denn Tante Anneliese musste immer auf Kruecken laufen und wenn mich meine Erinnerung nicht taeuscht, so war die Ursache dafuer die unter Anderem als Kinderlaehmung bekannte Krankheit. Diese war bis in die 60’er Jahre gefuerchtet, und entgegen des Namens sind auch Erwachsene vor dem Erreger nicht sicher.

Hier ist also eine Sache der ich noch persønlich begegnet bin; wenn auch am Rande und nicht in massiven Umfang. Gleichzeitig ist diese Krankheit aber von der Allgemeinheit im Wesentlichen vergessen wurde. Letzteres liegt natuerlich am massiven Erfolg der Impfstoffe und der nicht zu vergessenden, dazugehørenden, jahrzehntelang anhaltenden Impfkampagnen.

„Vergessen“ ist jetzt etwas harsch ausgedrueckt. Gerade im Zuge der Covidepidemie wurden die Erfolge des Impfens oft anhand des sehr starken Rueckgangs dieser Krankheit illustriert. Aber seien wir mal ehrlich. Das ist so, wie wenn von der Pest erzaehlt wird. Egal ob das 70 Jahre her ist oder 700. Der Schleier der Zeit macht tiefgreifendes Verstehen durch Erleben in beiden Faellen unmøglich.

Wie vormals, ist es auch in diesem Fall groszartig, dass wir, als Gesellschaft, uns dieses furchtbaren Schreckens nicht mehr wahrhaft bewusst sind. Wie ehedem, ist dies ein Ausdruck dafuer, wie weit die Menschheit es gebracht hat … dennoch (oder eigentlich gerade deswegen) sollten wir die Krankheit der sogenannten Kinderlaehmung und deren Folgen in Erinnerung halten.

Der schwarze Fleck vom vorletzten Mal suggeriert, dass die Anzahl der Links unabhaengig ist von der Anzahl der Zitierungen fuer Seiten mit weniger als 1000 Zitierungen.
Bei dieser Aussage schaute ich aber nur auf die individuellen Seiten (die vielen vielen vielen Punkte, die zusammen besagten schwarzen Fleck ergeben) und habe nicht die Anzahl der Seiten mit der gegebenen Anzahl an Zitierungen in Betracht gezogen. Dies war aber genau das, was ich beim letzten Mal bei der individuellen „Signalstaerke“ machte.
Wenn man nun die individuelle Signalstaerke durch die Anzahl der Seiten und die Anzahl der Zitierungen, bei der gegebenen Anzahl an Zitierungen teilt, dann erhaelt man die durchschnittliche Anzahl an Links in Abhaengigkeit von der Anzahl der Zitierungen. Das muss man so machen, wenn man die Anzahl der totalen Links auf LL₁ benutzt und ich erwaehne das hier, weil ich die ganzen vorherigen Artikel LL₁ diskutiert habe. Auf LL₀ muesste man natuerlich nur die Anzahl aller Links bei einer gegebenen Menge an Zitierungen, durch die Gesamtzahl der Seiten die so oft zitiert wurden dividieren. Egal wie man’s macht, DAS ist mal ein krasses Ergebniss:

Die Abhaengigkeit folgt einem maechtigen Gesetz mit dem Exponent 1/2 (zwei Grøszenordnungen auf der Ordinate, vier Grøszenordnungen auf der Abzsisse) und einem Vorfaktor von ungefaehr 7.5 .
Das erstaunliche hieran ist, dass dies im Wesenlichen fuer den gesamten (!) Bereich auf der Abzsisse gilt, also egal ob die Anzahl der Zitierungen klein oder grosz ist.
Ich schreibe „im Wesentlichen“, denn natuerlich gibt es Abweichungen. So kønnte man in absoluten Zahlen durchaus auch sagen, dass die Anzahl der Links pro Seite fuer kleine Zitierungen halbwegs konstant ist. Die Abweichungen vom maechtigen Gestz betragen dann ca. einen Faktor zwei, fallen also bei realen „Anwendungen“ nicht sooo sehr ins Gewicht.

Ab ca. 1000 Zitierungen scheint es dann gewaltige Abweichungen zu geben. Aber das taeuscht hier wieder durch die bereits beim letzten Mal erwaehnte „logarithmische Komprimierung“ und die Ueberlappung hunderter (tausender) von Punkten.
Es gibt 4,696 „Messwerte“ mit ueber 1000 Zitierungen. Diese kommen durch insgesamt 15,282 Seiten zustande. Allein hieran sieht man, dass etwaige Abweichungen in diesem Bereich nicht relevant sind fuer die (immer noch) fast 6 Millionen Wikipediaseiten, die anscheinend dem Gesetz „gehorchen“. Aber wir sind ja nun konkret an den Seiten mit mehr als 1000 Zitierungen interessiert.
Zur Veranschaulichung der Taeuschung møchte ich die folgenden Werte anfuehren. Zunaechst setze ich (willkuerlich) fest, dass eine Abweichung von drei als nicht mehr OK gilt. Das bedeutet, dass ich es als Abweichung zaehle, wenn der tatsaechliche Durchschnittswert dreimal grøszer oder weniger als 1/3 des vom maechtigen Gesetz vorausgesagten Wertes ist.
Dies ist der Fall fuer 976 „Messwerte“ und entspricht ca. 21 % aller „Messungen“ mit ueber 1000 Zitierungen. Andererseits kommen diese 976 „Messwerte“ nur durch 1,303 Seiten zustande. Letzteres entspricht dann nur noch ca. 8 Prozent aller Seiten mit ueber 1000 Zitierungen. Das faellt dann also wieder unter den beruehmten Zehn-Prozent-Fehler.
Wenn ich viel strikter bin und Abweichungen ab einem Faktor 2 zaehle so erhøht sich der erste Wert auf ca. 38 % und der letzte Wert auf ca. 21 %. Das ist mehr als eine „normale Fehlerbreite“ erwarten laeszt. Die Aussage, dass die Mehrheit der Seiten dem maechtigen Gesetz unterliegt wird dadurch allerdings nicht beeinflusst.
Ach so, wenn man alle Punkte mit in diese Ueberlegungen einbezieht, also auch die mit weniger als (oder gleich) 1000 Zitierungen so fallen (bei Faktor 3) immer noch ca. 17 % der Punkte unter die Rubrik „Abweichung“, aber diese kommen dann nur noch durch ca. 2 % aller Seiten zustande.

Ich sagte ja, dass dieses Resultat voll cool ist! Beim vorletzten Mal schrieb ich:

[…] in diesen [vielzitierten] Artikeln [ist] vermutlich jedes kleine bisschen verlinkt […]. Je populaerer ein Artikel ist, um so mehr beinhaltet dieser vermutlich, was dann wiederum zu mehr Links fuehrt.
Dennoch, dies war eine spannendes Resultat, eben weil mich das so ueberrascht hat.

Diese Aussage entstand aus einem Bauchgefuehl und fuehlte sich logisch und richtig an, auch wenn ich es nur fuer Artikel mit mehr als 1000 Artikeln einschraenkte. Das obige Ergebniss zeigt aber ganz deutlich, dass dies nicht fuer die gewaltige Mehrheit ALLER Artikel gilt. Vielmehr existiert eine ganz konkrete, quantifizierbare Gesetzmaeszigkeit dahinter. Das haette ich nicht erwartet und das ist, was ich so krass cool fand.

Und das ist dann die Freude des Forschers. Man guckt sich kleine Details an (wie bspw. ein Balken in einer Verteilung  der ein bisschen zu lang erscheint) und aus deren Erforschung ergibt sich eine allgemeine Gesetzmaeszigkeit fuer (mehr oder weniger) die gesamte Wikipedia! Geil wa!
Dies war definitiv einen eigenen Beitrag wert.

Aber Achtung! Das maechtige Gesetz gilt nicht zwangslaeufig fuer alle indivduellen Seiten. Der schwarze Block beim vorletzten Mal zeigte, dass die tatsaechliche Anzahl an Links einer Seite deutlich davon abweichen kann. Bei diesen Betrachtungen (und auch bei denen beim letzten Mal) werden individuelle Seiten unter dem Merkmal „Anzahl Zitierungen“ zusammengefasst. Und diese Ensembles verhalten sich im Durchschnitt wie oben angegeben! Das ist wie in der statistischen Mechanik, da betrachten wir auch keine einzelnen Atoemchen, sondern die potentiellen Zustaende eines System als Ganzes.

Ach so, das ist dann natuerlich der zweite Teil der Erklaerung, warum die rote „Gesamtsignalkurve“ im letzten Beitrag, trotz kleiner individueller Beitrage so stark ansteigt. Das sind zwar relativ wenige individuelle Seiten, aber die haben maechtig viel mehr Links.

Ich habe in den letzten zwei und diesem Artikel dargelegt, dass vielzitierte Seiten ueberproportonal zur Anzahl der Links von LL₁ zu LL₂ 2 beitragen. Beim naechsten Mal schliesze ich die Untersuchung dieses kleinen Details ab, mit einer Visualisierung, WIE gewaltig diese Ueberproportionalitaet wirklich ist.

… dass moderater Alkoholkonsum gut fuer einen ist.

Und noch mehr Zitate bzgl. Dingen die in ihrer Gesamtheit nicht sinnvoll sind, bzgl. dieser „Volksweisheit“, und ich zitiere auch heute wieder aus der (Literatur)Anaylse von Hans Olav Fekjær in Addiction 108 (12), pp. 2051–2057, 2013.

Ich hatte bereits kurz erwaehnt, dass Beobachtungsstudien ihre ganz eigenen Probleme haben. Fekjær drueckt das deutlich direkter und weniger diplomatisch aus (Hervorhebung(en) von mir):

The number of observational studies is not an indicator of the strength of the evidence for causal effect. Observational studies remain second-class evidence. This is also confirmed by the many studies giving unreasonable results.

Er gibt ein interessantes Beispiel bzgl. der „Beweiskraft“ von Observationsstudien:

One example is that television viewing is associated with higher cardiovascular and total mortality, independent of [!!!] physical activity, gender, age, education, smoking, alcohol, medication, diabetes history, family history of cardiovascular disease and cancer and body mass index […].

Wenn all das im obigen Zitat aufgefuehrte in Betracht gezogen wurde, dann stellt sich zu Recht die Frage:

[w]hy is TV viewing more harmful than, for instance, book reading?

Weil es nicht im Fernseh schauen selber liegen kann (denn dann waeren Fernseher und Monitore aller Art eine Gefahr fuer alle Menschen), muss es eine Eigenschaft der Gruppe der Vielfernsehschauer sein, die diese Ergebnisse plausibler erklaeren wuerden. In der Beobachtungsstudie kommt aber „Fernseh gucken“ raus. So weit ich weisz sind Beobachtungsstudien von sich aus verhaeltnismaeszig anfaellig fuer derartige … mhm … ich sag jetzt mal Fehler.

Davon unabhaengig ist auch die Klassifizierung von Menschen in Trinker und Nichttrinker problematisch. So tendieren Menschen dazu (deutlich) weniger zu trinken, so denn (generelle) Gesundheitsprobleme auftreten. Fekjær zitiert bspw. eine Studie die zu dem Schluss kommt, dass Ex-Trinker betraechtlich øfter vertreten sind unter den Todesfaellen durch Herz- und Kreislauferkrankungen. Entsprechend ist die …

[…] excess total or coronary mortality of non-drinkers […] found only in studies where ex-drinkers or occasional drinkers were included in the non-drinker group […].

Und nicht ueberraschend findet eine (andere) (Meta)Studie, dass…

[…] the apparent protective effect of alcohol disappeared when ex-drinkers and occasional drinkers were excluded from the non-drinker group […].

Das soll genug fuer heute und insgesamt dazu sein. Beim naechsten Mal dann eine (vielleicht) kurze und (vielleicht) knappe Zusammenfassung :)

Beim letzten Mal stellte ich die ersten Ergebnisse vor. Ein kleines Detail in der Verteilung der totalen Links pro Linklevel machte mich stutzig und fuehrte mich in einen Kaninchenbau voll interessanter Sachen. Es gibt viel zu viele Links die von Linklevel 1 zu Linklevel 2 fuehren — ich „messe“ eine „Signalstaerke“ von 27 Milliarden totalen Links von LL₁ zu LL₂.
Einfache Ueberlegungen fuehrten mich nicht weiter, aber halfen mir insofern, dass ich dadurch darauf aufmerksam wurde, dass mglw. vielzitierte Seiten einen ganz erheblichen Einfluss auf die Anzahl der totalen Links eines Linklevels haben. Ich schloss den Beitrag mit dieser Frage und direkten Handlungsanweisung ab:

[w]ie genau hilft uns dies nun aber mit der obigen Frage? [Wie stark der Einfluss vielzitierter Seiten auf das „Gesamtsignal“ ist.] Nun ja, das ist ganz einfach. Ich muss fuer jede Wikipediaseite das Produkt aus der Anzahl der Links und der Anzahl der Zitierungen bilden. Die Summer aller dieser Produkte sollte dann die ca. 27 Milliarden| totalen Links von LL₁ zu LL₂ ergeben.

Die Handlungsanweisung ist in der Gesamtheit natuerlich ganz klar und einfach. Die Entwicklung ueber die verschiedenen „Zitierungsniveaus“ fand ich aber ganz anschaulich (immer mit Blick darauf, dass uns diese Daten Dinge ueber das Linknetzwerk der Wikipedia erzaehlen) und møchte darauf heute kurz eingehen.
Mit Entwicklung meine ich das Folgende. Im ersten Schritt der Entwicklung schaue ich mir zunaechst die individuelle „Signalstaerke“ aller null Mal zitierten Seiten an. Individuell meint hier nicht jede Seite fuer sich, sondern alle null mal zitierten Seiten bilden ein „Individuum“ und die Links dieses „Individuums“ ergeben die „Signalstaerke“ im ersten Schritt. Im naechsten Schritt mache ich das gleiche fuer alle ein Mal zitierten Seiten; dann fuer alle zwei Mal zitierten Seiten usw. Das Ergebniss sind die schwarze Punkte in diesem Diagramm:

Die roten Quadrate sind die kumulative Anzahl aller Links von LL₁ zu LL₂ und die Kurve ist recht einfach zu verstehen als das „Gesamtsignal“ aller Beitrage bis zu dem gegebenen Punkt auf der Abzsisse. Aber der Verlauf der schwarzen Punkte ist interessant und bedarf einiger Worte

Vom letzten Mal wissen wir, dass bei Seiten die weniger als 1000 mal zitiert werden, die Anzahl der Links unabhaengig von der Anzahl der Zitierungen ist. Das bedeutet, dass eine Seite mit 10 Zitierungen um Durchschnitt gleich viele Links hat wie eine Seite mit nur einer Zitierung. Das ist nicht ganz richtig und darauf komme ich weiter unten nochmal zurueck, aber zur vereinfachten Rechnungn nehmen wir an, dass der Durchschnitt bei 10 Links pro Seite liegt.
Unter dieser Annahme ist es natuerlich einfach zu erklaeren, warum die schwarze Kurve zunaechst hoch geht. 1000 Seiten die einmal zitiert werden tragen zum Gesamtsignal 10-tausend Links bei. Die selbe Anzahl Seiten die 2 Mal zitiert werden tragen aber doppelt so viel zum Gesamtsignal bei usw. usf.
Von viel frueher wissen wir, dass die meisten Seiten ein Mal zitiert werden. Es gibt also weniger Seiten die zwei Mal, oder drei Mal usw. zitiert werden. Wenn man sich aber die Verteilung nochmal anschaut, dann sieht man, dass das nicht proportional weniger Seiten werden, deshalb der Anstieg der individuellen Signalstaerke. Waeren es proportional weniger Seiten in Abhaengigkeit von der Anzahl der Zitierungen, haette ich also bspw. nur halb so viele zwei Mal zitierte Seiten wie ein Mal zitierte Seiten, wuerde die Kurve der individuellen Signalstaerke flach verlaufen bei kleinen Zitierungen.

Bei ungefaehr 13 Zitierungen wird ein (lokales) Maximum erreicht und danach nimmt die individuelle Signalstaerke wieder ab. Das liegt daran, dass die Anzahl der Seiten mit mehr Zitierungen dann ueberproportional weniger werden. Mit der obigen vereinfachten Annahme denke man sich weiterhin, dass es nur 1 Seite gibt die 1000 Mal zitiert wird. Dann ist deren individuelle Signalstaerke genauso grosz (oder eher klein), wie die der 1000 Seiten die ein Mal zitiert werden.
Erst bei sehr vielen Zitierungen kehrt sich dieser Trend dann wieder um, nicht zuletzt dadurch, weil vielzitierte Seiten im Durchschnitt auch mehr Links enthalten.

Nun ist aber zu erklaeren, warum die rote Kurve zunaechst einen so geringen Ansteig hat und erst nach dem lokalen Maximum stark ansteigt? Letzteres trotz der geringen individuellen Signalstaerken.
Zum Einen liegt das an der Komprimierung durch die logarithmische Achse. Zwischen einer und 10 Zitierungen (inklusive) liegen 10 Datenpunkte; zwischen 100 und 1000 Zitierungen liegen 900 Datenpunkte. Auf der Abzsisse nehmen die aber den gleichen Raum ein. Wenn man 10 Datenpunkte zur kumulativen Anzahl an Links aufsummiert ergibt das natuerlich einen geringeren Beitrag als wenn man 900 Datenpunkte aufsummiert.

Aber das ist nur ein Teil der Erklaerung. Der andere Teil ist, dass die obige Annahme nicht richtig ist. Vielmehr ist die Anzahl der Links eben doch abhaengig von der Anzahl der Zitierungen auch bei kleinen Werten. Das ist bei der Darstellung vom letzten Mal nicht zu sehen und dieses Ergebniss ist sehr spannend, denn es sagt wieder viel ueber die Wikipedia aus. Aber weil der Artikel jetzt schon so lang ist, verschiebe ich die Diskussion auf’s naechste Mal.

… dass moderater Alkoholkonsum gut fuer einen ist.

Es folgen weitere Zitate bzgl. der Ungereimtheiten rund um diese „Volksweisheit“, aus der (Literatur)Anaylse von Hans Olav Fekjær in Addiction 108 (12), pp. 2051–2057, 2013.

Beim letzten mal erwaehnte ich, dass leicht und moderat trinkende Menschen, optimal in die Gesellschaft integriert sind und dass wahrscheinlich dies (und nicht der moderate Alkoholkonsum) die positive Auswirkungen auf die Gesundheit erklaert. Da ist es dann natuerlich naheliegend zu fragen, wie es den Menschen so geht, die nix trinken.
Historisch gesehen war das mal eine recht breite Bevølkerungsgruppe. Heutzutage sind’s ’n paar Prominente und „komische Vøgel“ … und viele „unsichtbare“ Menschen. Und um Letztere geht es heute, denn …

[t]oday’s abstainers are, […] not an average group of people who happen to have a temperance conviction, but are more often a somewhat deviant and marginalized group.

Leider schlaegt sich das im Durchschnitt auf die Lebensfuehrung nieder und …

[…] abstainers generally have less favourable life-styles than light or moderate drinkers.

So ist es bspw. so, dass …

[a]bstainers as a group have a less healthy diet and exercise less than moderate drinkers […].

Aber …

[t]hese key confounders are rarely mentioned in the observational studies.

Nun ist es aber so, dass man schlechte Ernaehrung und wenig Bewegung als „Størfaktoren“ mit in Betracht ziehen kann. Aber selbst denn gilt, dass  …

[e]ven when all known confounders are taken into account, psychosocial factors seem to have a considerable impact on morbidity and mortality, probably through mechanisms which are still unknown. One study concluded that abstainers have more of several psychosocial risk factors such as low education, passive life-style, being unmarried, disabled or depressed […].

Und das hat mich ueberrascht. Aber ausgehend von mir, haette mich das nicht ueberraschen sollen. Ich leide zwar z.Z. nicht unter einer Depression, bin nicht eingeschraenkt in meinen kørperlichen Funktionen und wuerde sagen, dass meine (formale) Bildung relativ „hoch“ ist, aber der Rest passt (leider) durchaus. Da war ich natuerlich blind meinem eigenen, ungesunden Lebensstil gegenueber (ich fuehl mich doch gut!). Auszerdem frage ich mich, ob das anders waere, wenn mich bspw. wer zum klettern (oder ins Trainingsstudio) mitgenommen haette, oder wenn ich einmal pro Monat (oder mglw. gar Woche) soziale Zusammenkuenfte haette, die mich inspirieren wuerden, besser zu essen. Die Studien sagen dazu: JA, denn gute, soziale Integration hat schon seine Vorteile. Im Zusammenhang mit dem Thema dieses Artikels bedeutet dies …

[…] abstainers have fewer and poorer social relationships […] [and] [d]ata across 308 849 individuals […] [shows] that individuals with adequate social relationships have a 50% greater likelihood of survival compared to those with poor or insufficient social relationships. The magnitude of this effect is comparable with quitting smoking and it exceeds many well-known risk factors for mortality (e.g. obesity, physical inactivity) […].

Kein Wunder, dass es in Beobachtungsstudien scheint, als ob es schlecht fuer die Gesundheit ist, wenn man gar keinen Alkohol trinkt. Das hat aber vermutlich nichts mit dem Alkohol zu tun.

… dass moderater Alkoholkonsum gut fuer einen ist.

Weiter geht’s mit den Merkwuerdigkeiten rund um diese Volksweisheit, ueber die Hans Olav Fekjær in Addiction 108 (12), pp. 2051–2057, 2013 in der (Literatur)Analyse mit dem Titel „Alcohol—a universal preventive agent? A critical analysis“ schreibt.

Somit ohne viel Aufhebens:

Alcohol apparently prevents12 diseases among the 16 listed by Wikipedia as ‘lifestyle diseases’.

Wikipedia ist ein „lebendes Dokument“ und ich finde da mittlerweile 21 Lebensfuehrungskrankheiten, aber die Aussage ist klar. Weiter geht es damit, dass …

[t]he level of consumption which seems to have a preventive effect is the level that is most accepted in our present-day societies, more socially accepted than both abstention and higher consumption.

Zur Abstinenz komme ich beim naechsten Mal, aber der Punkt, dass …

[…] the [societal] group consuming alcohol at this level is conforming to the currently prevailing norms

… ist wichtig, denn …

[n]ot surprisingly, several favourable characteristics have been demonstrated for this group. It differs from abstainers in many lifestyle factors which are relevant for health

Konkreter zitiert Fekjør eine andere Studie:

[…] ‘wine drinking is a general indicator of optimal social, cognitive, and personality development […]. Similar social, cognitive, and personality factors have also been associated with better health in many populations. Consequently, the association between drinking habits and social and psychological characteristics, in large part, may explain the apparent health benefits of wine’.

Interessanterweise kann man das relativ leicht testen, denn fast alle Studien zu moderatem Alkoholkonsum und positiven Gesundheitseffekten wurden in „westlichen“ Laendern durchgefuehrt, in denen moderate Trinker im Durchschnitt einen høheren sozialen Status haben. Im Einklang mit den Ergebnissen von Holmes et al. folgerte …

[…] a study in India […] that light drinking increased the risk of coronary disease.

Der Schluss liegt nahe, dass dies vermutlich daran liegt, dass in der gesamten indischen Gesellschaft niemand erwartet, dass religiøse Hindus Alkohol trinken. Diese sind im Durchschnitt also nicht schlechter dran als Nichttrinker in westlichen Laendern.

Zusammenfassend kann diesbezueglich also gesagt werden, dass

[a]ltogether, there is ample evidence that groups with different drinking habits differ in several other ways than their drinking, making it difficult to separate the effects of drinking habits from other factors.

So viel dazu, naechstes Mal dann, wie viel schlechter es Abstinenzler in westlichen Laendern im Durchschnitt haben. Eine Sache, die mich doch etwas ueberrascht hat.

Das Folgende ist euch, meinen lieben Leserinnen und Lesern mglw. gar nicht aufgefallen beim Lesen der (bereits øfter zitierten) Studie von Holmes, M. V. et al. in BMJ, 2014; 349:g4164, denn es ist ein bisschen (in Tabelle 1) versteckt:

Nichtmal theoretische Physiker (also Physiker die eher theoretisch als experimentell arbeiten, nicht die Menschen, die theoretisch Physiker sein kønnten) arbeiten mit Werten die angegeben sind mit 76 Stellen nach dem Komma.

Ich weisz, dass das bei den Formeln zur Statistik rausfaellt, wenn man wirklich viele Probanden hat. Das ist mir selber schon passiert, wenn auch nicht ganz so extrem. Ich fand’s aber trotzdem lustig zu sehen und mir kam der Gedanke, dass wenn die Autoren der Studie einen normalen Taschenrechner mit 10 Stellen gehabt haetten, die Genauigkeit viel kleiner gewesen waere  … tihihi.

… dass moderater Alkoholkonsum gut fuer einen ist.

Ich bin ueber noch einen wissenschaftlichen Artikel gestolpert mit dem passenden Titel „Alcohol—a universal preventive agent? A critical analysis“ von Hans Olav Fekjær in Addiction 108 (12), pp. 2051–2057, 2013 … ich sehe gerade nicht, ob der frei zugaenglich ist, weil ich in der Unibibo in Uppsala sitze; falls nicht: *hust*.

Hier schrieb ich:

[…] der […] Selkorrekturmechanismus der Wissenschaft […] [benøtigt] meist viele und lange und teure Studien […] oder die Entwicklung einer neuen Methode […].

Die in den letzten Beitraegen besprochene Studie von Holmes et al. benutzte eine neue Methode, wohingegen die hier zitierte (Literatur)Analyse den anderen Weg geht. Und das ist der Grund, warum ich besagten Artikel so interessant finde und die Resultate in mehreren kuerzeren Beitraegen vorstellen werde. Auszerdem ist’s immer gut Argumente gegen weitverbreitete Dummheiten zur Hand zu haben.

Deswegen leg ich jetzt ohne weitere lange Rede auch gleich mit der ersten (Meta)Beobachtung los.

Fekjær listet eine Auswahl von 45 (Beobachtungs)Studien auf, die scheinbar einen Zusammenhang zwischen leichten/moderatem Alkoholkonsum und dem Schutz vor 26 Krankheiten nachweisen. Die Krankheiten sind so unterschiedlich wie Alzheimer, Asthma, Darmkrebs, Diabetes, Gallensteine, niedriges Geburtsgewicht (!), Uebergewicht, Krankheiten des Geistes und ueberhaupt allgemeine Sterblichkeit. Ganz zu recht schreibt der Autor dann:

[a] conspicuous fact is that light or moderate drinking apparently prevent such a large number of unrelated diseases.

Denn das ist tatsaechlich auffaellig. Und noch mehr auffaellig ist, dass …

[…] beneficial effects for the different diseases all seem to peak at approximately the same consumption level. […] [I]n practically all these studies, certain small doses of alcohol appear to be protective and somewhat larger doses are apparently harmful.

Die Abhaengigkeit der „Reaktion“ einer Krankheit von der Dosis einer Medizin ist bekannt. Diese Dosisabhaengigkeit funktioniert aber nicht so wie Alkohol scheinbar funktioniert. Vielmehr kann der „Dosisgrenzwert“ ab dem ein Medikament nicht mehr hilft und eher schaedlich wird weit fluktuieren von Mensch zu Mensch und natuerlich von Krankheit zu Krankheit.
Nicht so bei Alkohol, da ist’s immer die (mehr oder weniger) gleiche Dosis, die dich gegen alles gleichzeitig beschuetzt … und das ist tatsechlich sehr verdaechtig in die Richtung, dass leichter/moderater Alkoholkonsum mglw. Ausdruck fuer was ganz Anderes ist und nicht wirklich gegen Krankheiten schuetzt (Letzteres ist ja was Holmes et al. direkt nachweisen).

Dazu mehr beim naechsten Mal.

Zum Jubilaeum (heute vor einem Jahr erschien der allererste Beitrag in dieser nicht ganz so kurzen Miniserie) geht es endlich mal weiter mit Kevin Bacon. Auch wenn die Weise der Publizierung das nicht erkennen laeszt, so habe ich die Auswertung doch monatelang vor mich hergeschoben, weil das so viel ist.

Heute nun steige ich gleich voll ein und verliere mich in einer Sache, die zunaechst wie ein kleines, nicht ganz so wichtiges Detail aussieht. Zumindest erschien es mir so. Dann machte ich aber ein paar Ueberschlagsrechnungen und irgendwie stimmte das Hinten und Vorne nicht. Die Aufklaerung des Mysteriums war eine spannende Sache und legt dann bereits ganz am Anfang SEHR viel ueber das Linknetzwerk der Wikipedia dar.
Das ist als eine Art „Warnung“ anzusehen, dass dies ein laengerer Beitrag wird.

Als kurze Wiederholung:
– Ich rede von Linkleveln und die Nummer des Linklevels sagt aus, wie viele „Schritte“ ich im Linknetzwerk getan habe um dort hinzukommen.
– Die Linklevel fangen an bei Null zu zaehlen, was dann natuerlich dem Titel / der Wikipediaseite entspricht, dessen Linknetzwerk ich jetzt gerade untersuche.
– Links die in vorherigen Schritten besucht wurden, werden nicht nochmal besucht.
– Auf jedem Linklevel sammle ich Daten und heute geht es um die totale Anzahl von Links die zum naechste Linklevel fuehren. Siehe dazu mein Artikel von neulich (gut, dass ich den geschrieben habe).
– Ich bin i.A. nicht an einzelnen Seiten interessiert, sondern an der Gesamtverteilung der Grøsze(n) von Interesse ueber alle Titel.

Und nun geht’s los und immer schøn der Reihe nach.

In der Gesamtheit sieht die Verteilung der totalen Anzahl von Links per Linklevel ueber alle Wikipediaseiten so aus:

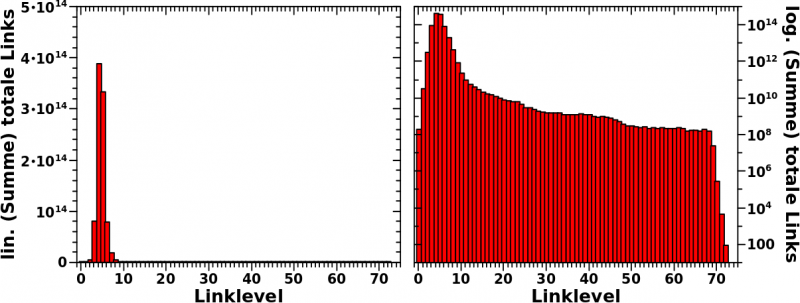
Das sieht einfach aus, denn Verteilungen hatte ich hier ja schon ein paar Mal. Aber wenn man das auf sich wirken laeszt, dann sind da eine Vielzahl von Beobachtungen. Viele dieser Beobachtungen sind allgemein und treten auch so, oder zumindest in aehnlicher Form, bei anderen Grøszen von Interesse auf. Weil wir, also ihr, meine lieben Leserinnen und Leser, und ich, dem hier zum ersten Mal begegnen, møchte ich etwas naeher darauf eingehen.

Wie so oft sehen wir, dass die Darstellung mit linearer Ordinate im linken Bild nicht viel hergibt. Andererseits sehen wir bei lineraer Darstelung, wie schnell alles passiert und dann auch wie schnell alles wieder vorbei ist. Das Maximum ist nach nur vier Schritten erreicht. Und bereits auf Linklevel 3 tuen sich fast 100 Billionen Links auf. Das heiszt bei ca. 6 Millionen Titeln, habe ich nach nur 3 Schritten im Durchschnitt bereits ca. 150 Millionen weiterfuehrende Links vor mir.
Das erklaert natuerlich, warum man die meisten Titel von jedem anderen Titel mittels nur drei (oder vier) Schritten erreichen kann. Das war ja eine ganz konkrete Sache, ueber die ich mich bereits im allerersten Beitrag dieser Reihe (wenn auch nicht direkt) wunderte und die in mir ueberhaupt erst das Interesse an dem ganzen Thema weckte. Damit waere das nach einem Jahr dann endlich geklaert. Toll wa!

Bei logarithmischer Ordinate sieht man dann aber, dass auch nach dem Maximum noch laengst nicht alles vorbei ist. Und ach du meine Guete! Die Dynamik in dieser Verteilung geht von (knapp unter) 100 bis 10¹⁴ … das sind 12 Grøszenordnungnen! Das ist so viel, dass ich hier nicht mal mehr die kleinen Striche an der Achse zeichne. Dabei finde ich die doch so toll, weil sie so charakteristisch fuer logarithmische Achsen sind :) .
In Zukunft werde ich Verteilungen mit lineare Ordinaten nur noch zeigen, wenn es zu Informationsgewinn fuehrt. Bei einer solchen Dynamik ist es ziemlich offensichtlich, dass die logarithmische Darstellung der linearen ueberlegen ist.

Auch wenn das Allermeiste nach Linklevel 8 vorbei, so sieht man auch, dass es Wikipediaseiten gibt, die noch viel mehr Schritte benøtigen, bevor man diese erreicht hat. Hier nehme ich dann meine Aussage von oben teilweise zurueck und sage, dass mich dann doch interessiert, welche Seiten das sind.
Aber auch die letzte Ecke des Weltwissens ist nach maximal 73 Schritten erreicht. Der letzte Balken ist auf Linklevel 72 und das bedeutet, dass es nur noch von dort „Ausgaenge“ zu Seiten gibt, die ich vorher nicht besucht habe. Dies wird aber an anderer Stelle genauer betrachtet.

Das sind allgemeine Sachen. Heute von Interesse ist nur das Maximum (man beachte, dass die Ordinate nicht bei Null, sondern erst bei 10 Millionen anfaengt; die Balken sind also „eigentlich“ viel laenger) …

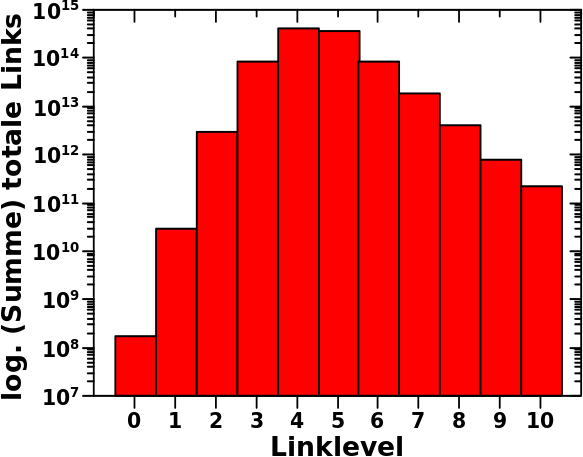
… und eigentlich interessiert mich gar nicht das Maximum an sich, sondern nur der Aufstieg von Linklevel 1 zu Linklevel 2 … und was dies ueber das Linknetzwerk sagt. Aber der Reihe nach.

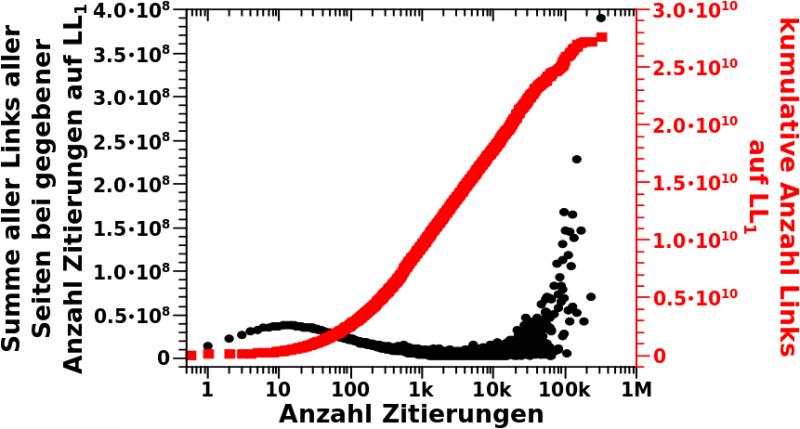
Auf Linklevel 0 … ach je, das wird mir zu umstaendlich das immerzu zu schreiben und ich kuerz das jetzt mit „LL“ ab und der Wert ist dann der Index … jedenfalls betraegt die Summer der totalen Links auf LL₀ 165,913,569. Diese Zahl kenne wir schon, denn es ist die Summe aller Links, die ich auf allen Wikipediaseiten finde. Zum ersten Mal sind wir auf diese Zahl bereits vor langer Zeit gestoszen.
Wenn ich nun diese ca. 165 Millionen „Ausgaenge“ zu LL₁ nehme, dann treffe ich dort auf mehr als 27 Milliarden Links. Cool wa, wie schnell das waechst! … … … Moment mal! … wieso waechst das denn SO schnell? … Das kommt mir etwas komisch vor.

Und damit sind wir bei dem am Anfang erwaehnten Detail, welches leicht zu uebersehen ist.

Machen wir mal eine Ueberschlagsrechnung. Die ca. 165 Millionen Links auf LL₀ verteilen sich auf ca. 6 Millionen Seiten. Das macht ca. 30 Links pro Seite im Durchschnitt … nicht ganz, aber es ist ja nur eine Ueberschlagsrechnung. Wenn ich nun 165 Millionen Seiten auf LL₁ mit (durchschnittlich) 30 Links pro Seite multipliziere, dann komme ich auf ca. 5 Milliarden „Ausgaenge“ zu LL₂.
Einen Faktor zwei haette ich mglw. als „Fehler“ abgetan, aber ’n Faktor 5 zu viel? Hier scheint ein nicht ganz so offensichtlicher Mechanismus zu wirken … SUPERSPANNEND!

Aber vielleicht ist es doch ganz einfach. Denn mglw. muss ich mit dem Median und nicht dem Mittelwert rechnen … da muss ich mal eine der aelteren Analysen raussuchen … *raussuch* … im Wesentlichen ist’s das hier … øhm … nø … das ist auch nicht des Raetsels Løsung, denn die Haelfte der Seiten haben 15 Links oder weniger … Mhmmmmm … aber Moment … wenn der Mittelwert bei ca. 30 liegt, dann bedeutet das doch, dass Seiten mit (deutlich) mehr als 30 Links pro Seite einen groszen Einfluss haben muessen … mhmmmmm …

Einschub: die Idee mit dem Median war, wenn man mal drueber nachdenkt, von Anfang an zum Scheitern verurteilt … aber das Resultat dieser Idee (der relativ grosze Unterschied zwischen Median und Mittelwert) fuehrte mich letztlich in die richtige Richtung … das ist das Schøne am Erforschen eines Themas … das klappt mitnichten alles beim ersten Mal, aber wenn man was probiert was zu nix fuehrt, wird man mitunter auf Details aufmerksam, die man so vorher gar nicht bemerkt hat … und dann kommt man ueber einen (mehr oder weniger) kurzen Umweg doch noch zur Løsung :) .

Da stellt sich nun die Fragen: wie grosz ist eigentlich der Einfluss vielzitierter Seiten?
Ich stellte die 50 meistzitierten Seiten bereits vor. Und eine Seite, die bspw. 1000 Links hat und 300-tausend Mal zitiert wird, wuerde zum Gesamtsignal 300 Millionen Links — also ca. 1 % — beitragen. Gleichzeitig wissen wir, dass das Maximum der Verteilung der Zitierungen bei eins liegt, waehrend das Maximum der Links pro Seite bei ca. 10 liegt. Diese zwei Dinge zusammen fuehren dazu, dass ich fuer die gleiche Signalstaerke die die 300-tausend Mal zitierte Seite hat, 30 Millionen Seiten braeuchte, die ein Mal zitiert werden (mit 10 Links pro Seite). So viele gibt es gar nicht und um besagte Signalstaerke zu erreichen muesste ich alle Seiten zusammen nehmen, die einmal, zweimal, dreimal, … neunmal, zehnmal zitiert werden.
Diese kurze und einfache Ueberlegung zeigt bereits, wie krass ueberproportional der Einfluss nur einer vielzitierten Seite sein kann. Aber die 1000 Links oben habe ich mir nur ausgedacht und es stellt sich die naechste Frage: wie sieht denn die Anzahl der Links in Abhaengigkeit von den Zitierungen aus?

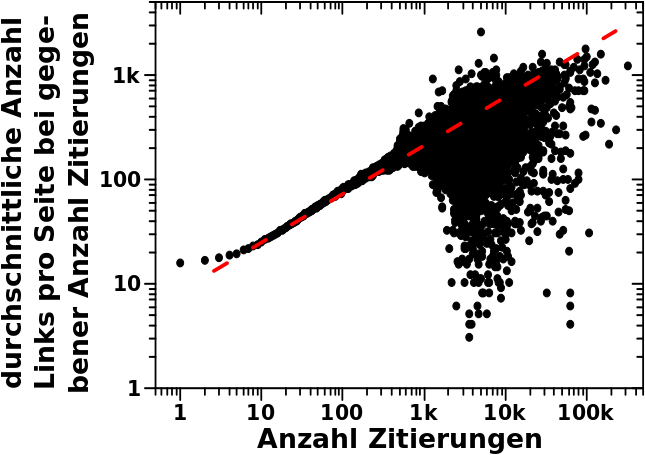
Nun ja, das ist etwas unuebersichtlich und sieht so aus:

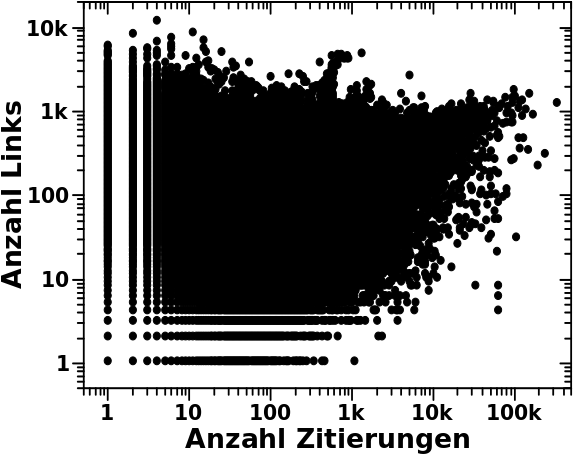
Wir sehen, dass wir erstmal nix sehen, auszer einem groszen schwarzen Fleck.
Der schwarze Fleck kommt durch die Ueberlappung sehr sehr sehr vieler Datenpunkte zustande. Wobei ich die Punkte fuer null Zitierungen bzw. null Links weggelassen habe, weil die hier nicht relevant sind.

Wenn man sich alles mal genauer anschaut, dann sieht man, dass die Seite mit den meisten Zitierungen tatsaechlich ca. 1000 Links hat. Das war aber reiner Zufall.
Desweiteren sieht man, dass Wikipediaseiten selten deutlich mehr als 1000 Links haben und dass die Anzahl der Links unabhaengig ist von der Anzhal der Zitierungen fuer Seiten die weniger als ca. 1000 Zitierungen auf sich vereinen.
Ab ca. 1000 Zitierungen haben die entsprechenden Seiten aber anscheinend eine Art „Mindestanzahl“ an Links, in Abhaengigkeit von der Anzahl der Zitierungen. Das sieht man an der schraeg liegenden „Abbruchkante“, welche die „Mindestanzahl“ an Links festlegt, die eine Seite haben „muss“, wenn sie bspw. 50-tausend Zitierungen auf sich vereint.
Das war erstmal ein _aeuszerst_ (!) ueberraschendes Ergebniss. Damit hatte ich nicht gerechnet. Ohne weitere Vorannahmen gibt es dafuer auch gar keinen Grund, denn warum sollte eine vielzitierte Seite nicht nur einen Link haben. Und das sieht man ja auch bspw. an den drei vertikalen Punkten bei ca. 60-tausend Zitierungen. Das sind drei so oft zitierte Seiten mit weniger als 10 Links.
Andererseits ist dieses Ergebniss dann doch nicht so ungewøhnlich wenn man bedenkt, dass vielzitierte Seiten vermutlich (eben wegen deren Popularitaet) sehr gut kuratiert sind. Das bedeutet dann, dass in diesen Artikeln vermutlich jedes kleine bisschen verlinkt ist. Je populaerer ein Artikel ist, um so mehr beinhaltet dieser vermutlich, was dann wiederum zu mehr Links fuehrt.
Dennoch, dies war eine spannendes Resultat, eben weil mich das so ueberrascht hat.

Wie genau hilft uns dies nun aber mit der obigen Frage? Nun ja, das ist ganz einfach. Ich muss fuer jede Wikipediaseite das Produkt aus der Anzahl der Links und der Anzahl der Zitierungen bilden. Die Summer aller dieser Produkte sollte dann die ca. 27 Milliarden| totalen Links von LL₁ zu LL₂ ergeben.

Aber an dieser Stelle breche ich ab. Es muss noch ziemlich viel erklaert werden und der Beitrag ist jetzt schon so lang.

… dass moderater Alkoholkonsum gut fuer einen ist.

(Vor)Letztes mal schrieb ich, dass Holmes, M. V. et al., in ihrer Studie „Association between alcohol and cardiovascular disease: Mendelian randomisation analysis based on individual participant data“ in BMJ, 2014; 349:g4164, herausfanden, dass Traeger der rs122984 Mutation des ADH1B Gens bessere Werte bei den Biomarkern haben, die mit Herz-Kreislauferkrankungen in Verbindung stehen. Ich liesz offen, ob sich das auch auf tatsaechliche Faelle koronarer Herzkrankheiten (hier scheint die dtsch. Wikipedia mal brauchbar zu sein) durchschlaegt … jaja, ich uebertreibe etwas im Titel dieses Beitrags, aber letztlich fuehrt das doch alls zu Herzinfarkten, nicht wahr.

Ohne viel Aufhebens, das Ergebniss ist, dass durch die Bank weg…

[…] [mutants] showed reduced odds of coronary heart disease […].

Auch die Einteilung der Personen in Gruppen (um den Zusammenhang zur „Volksweiheit“ herzustellen) aenderte daran nix:

[f]urther subdivision of the drinkers category into light (>0 to <7 units/week), moderate (≥7 to <21 units/week), and heavy (≥21 units/week) showed the same protective effect of the variant across all alcohol categories […].

Das ist also komplett entgegen besagter „Volksweisheit“ — egal wie viel (oder wenig) man trinkt, dass ist immer schlechter fuer dich, als nicht zu trinken. Oder anders:

[f]rom the U shaped association seen in observational studies, we would expect that for drinkers below the nadir (12-25 units/week), a reduction of 17.2% in alcohol consumption (corresponding to […] [be a mutant]) would lead to a small increase in the risk of coronary heart disease […]. Contrary to these expectations, however, we found that individuals below the nadir with a genetic predisposition to consume less alcohol had lower odds of developing coronary heart disease at all categories of alcohol consumption […] bringing the hypothesised cardioprotective effect of alcohol into question.

Der letzte Satz ist natuerlich sehr diplomatisch ausgedrueckt … tihihi.

Ganz wichtig war auch das Ergebniss bzgl. der beim letzten Mal erwaehnten Kontrollgruppe.

When analysis was restricted to non-drinkers the association was null […]

Es gab also keine Assoziation mit koronaren Herzkrankheiten und der Mutation bei Nichttrinkern. Das ist so wichtig, denn dies „koppelt zurueck“ zu der Annahme auf der die Benutzung der Methode der Mendelschen Randomisierung beruht:

[t]his is consistent with the assumption that the associations ascribed to the ADH1B variant are mainly due to alcohol consumption.

Also NICHT weil die Mutation auch noch irgendwas anderes im Kørper macht.

Lange Rede kurzer Sinn: wenn man das ordentlich untersucht und nicht nur schaut ob (und wie viel) Leute mit bestimmten Krankheiten Alkohol trinken, dann kommt man zu dem Schluss, dass auch leichter oder moderater Alkoholkonsum ganz generell nicht gut fuer dein Herz-Kreislaufsystem sind.

Soweit genug zum Artikel von Holmes et al. Das beendet die Reihe aber nicht, weil ich im Zuge dieser Fragestellung auf einen anderen Artikel gestoszen bin, in dem ein paar andere Dinge besprochen werden, die in den letzten Jahren Zweifel an der Gueltigkeit dieser „Volksweisheit“ aufkommen lieszen. Waehrend Holmes et al. eine (mehr oder weniger) neue Methode (und krass viele Daten) benutzen, so gehen die Argumente des besagten Artikels in eine andere Richtung. Das faellt aber auch unter den Mechansimus der „Selbstkorrektur in der Wissenschaft“ und deswegen møchte ich das gerne vorstellen. Und dann liefert es natuerlich noch mehr gute Argumente gegen die staendige Wiederholung dieser gefaehrlichen „Volksweisheit“ bei der naechsten sozialen Zusammenkunft.