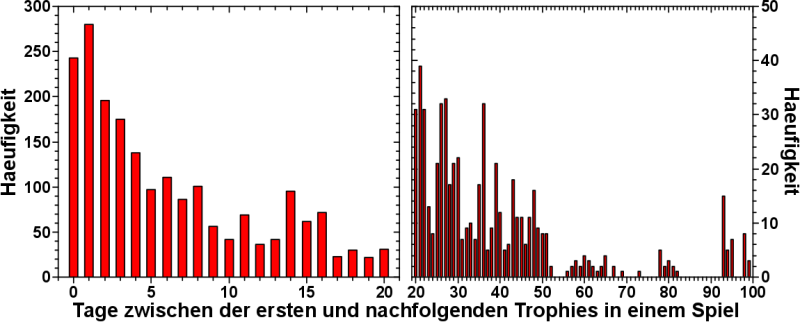
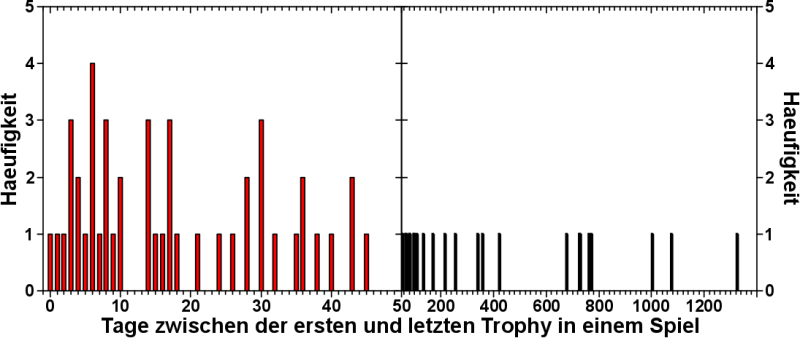
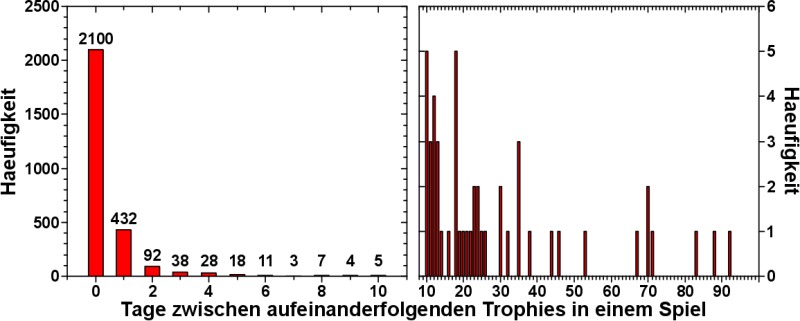
Es ist erstaunlich (durchaus im positiven Sinne gemeint), wie viele interessante Daten gesammelt werden, auf die wir auch Zugriff haben.
Ueber diese Erstaunlichkeit stolperte ich, als mich die Frage „Wie viele aus meinem Geburtsjahrgang sind eigentlich schon tot“ so sehr beschaeftigte, dass ich mir die Muehe machte, mal danach zu suchen.
Und da liegt dann auch die eigentliche Schwierigkeit. Der Datenreichtum ist so unuebersichtlich! Ich brauchte 2 1/2 Stunden, bis ich endlich diese ganz spezifische Information fand. Dann brauchte ich eine halbe Stunde, bis ich wirklich verstanden hatte, was ich da eigentlich sehe. Schlussendlich kam da noch fast ’ne Stunde dazu, bis ich aus den vielen Zahlen die Information derart extrahiert hatte, sodass ich die hier praesentieren kann. Also im Wesentlichen die selbe Situation wie hier.
Wieauchimmer, zunaechst einmal brachte ich in Erfahrung, dass in Deutschland (Ost und West zusammen) im Jahre 1980 die Anzahl der lebend geborenen Kinder 865.789 betrug. Hier ist die Datengrundlage dazu. Dort dann „Demography and migration“, dann „Fertility“ und da dann „Live births (total) by month“ selektieren. Dann auf das „Data explorer“-Icon klicken und nach druecken auf eins der „+“ Symbole die im Kopf der Tabelle erscheinen kann man waehlen, welche Daten man sehen will. (Direktlink, weisz aber nicht, ob das bei euch, meinen lieben Leserinnen und Leser, funktioniert)
Leider wurde 1980 noch nicht aufgeschluesselt welches (physische) Geschlecht diese Kinder hatten.
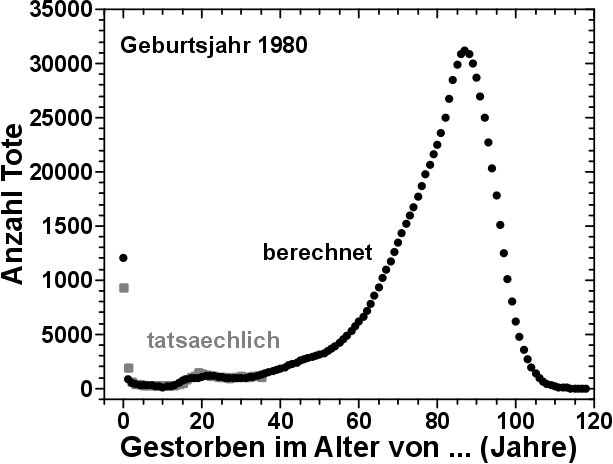
Tja … und dann ging das Sterben los:
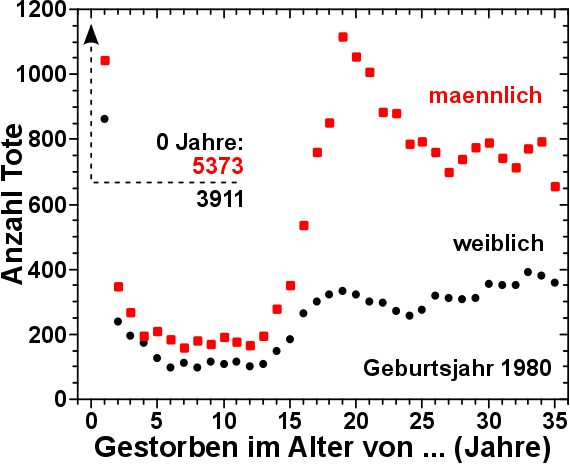
Datengrundlage, „Demography and migration“ => „Mortality“ => „Deaths by year of birth (age reached) and sex“, Direktlink
Zunaechst ist zu sagen, dass signifikant viele Menschen sterben, bevor sie das erste Lebensjahr erreichen. Aus dem Jahrgang 1980 waren das fast 10.000 Kinder. Diese Zahl liegt heute bei ca. einem viertel des damaligen Wertes (bei ca. 85 % so vielen geborenen Kindern in 2015).
Und auch im ersten Jahr ist die Sterberate noch signifikant erhøht, nimmt aber bis zum 5. Lebensjahr zunaechst rapide, dann langsamer ab.
So harsch das klingen mag, aber ich nehme an, dass dies dann wohl die Evolution ist, die da wirkt.
Dann sterben Jungs/junge Maenner bis zum ca. 13 Lebensjahr geringfuegig øfter als Maedchen/junge Frauen. Aber das ist ja ein bekannter Fakt, dass menschliche Maennchen anfaelliger fuer alles møgliche sind. Die Evolution gleicht das ja dadurch aus, dass von 100 % neuen Kindern ca. 51 % Jungs sind.
Dann kommt die Pubertaet und mit ihr der Fakt, dass der fuer das „erst denken dann handeln“-Teil des Gehirns sich bei Jungs spaeter entwickelt als bei Maedchen. Und so weit ich weisz geht die Forschung tatsaechlich davon aus, dass dumme Handlungen — Mutproben, Saufen, zu schnelles Mopedfahren etc. — fuer die signifikant høhere Sterberate bei den Jungs und jungen Maennern verantwortlich ist. Leider kann ich keine Literaturangabe dazu liefern. Ich speicher ja auch nicht alles was ich lese.
So ab Anfang 20 ist die Pubertaet dann aber vorbei. Die Sterberate unter Maennern geht zurueck und pegelt sich auf einem ungefaehr konstanten Wert ein, bleibt aber immer noch deutlich høher als bei den Frauen. Die Erklaerung dafuer ist mglw. wieder „das schwache Geschlecht“.
Schlussendlich kann man ab ca. 25 Jahren einen leichten, aber stetigen, Anstieg der Sterberaten erkennen. Das ist dann vermutllich „das Alter“. Oder anders ausgedrueckt: Die Mutationen kumulieren sich und dann landet man rein statistisch in der Krebsstatistik.
Man kann nur versuchen, sich aus bestimmten Krebsstatistiken raus zu halten. Aber das gelingt nicht immer, wie bspw. die Lungenkrebsfaelle zeigen. Einer von 10 Lungenkrebsfaellen entsteht bei Menschen die nicht rauchen (gar nie geraucht haben). Auch hier muss ich die Quelle dieser Aussage leider schuldig bleiben.
So … wieviele Personen die 1980 in Dtschl. geboren wurden, sind denn nun schon gestorben? An dieser Stelle betrachte ich dann Feinheiten a la „im Ausland gestorben“ oder „nicht 1980 in Dtschl. geboren“ mal nicht.
Die nachrechnenden Leserinnen und Leser werden es bemerkt haben: die Zahl ist der Titel dieses Beitrags.
Runden wir das auf 5 % auf, dann kann man mal ueberlegen, wer aus der ehemaligen Schulklasse denn schon tot ist.
Bei mir sind’s schon 2. Ich liege also ueber’m Durchschnitt. Leider gibt es sowas wie „ausgleichende Gerechtigkeit“ nicht, Sterben ist meist unkorelliert … mhm … aber Kriege oder Generationenplagen wie „Rauchen“ oder das Mutprobendingens waehrend der Pubertaet … oder … oder … oder … vielleicht ist Sterben oft genug doch korelliert, sodass ich diese Aussage lieber zurueck ziehe; aber der erste Teil des Satzes bleibt natuerlich bestehen.
Tja … 5 % … das hørt sich ja nicht so viel an. Deswegen schauen wir uns mal die sogenannte „Life table“ aus dem selben Datensatz (unter „Mortality“, Direktlink) an.
In einer „Life table“ ist die altersspezifische Sterbewahrscheinlichkeit angegeben (bezogen auf die noch nicht gestorbenen Menschen). Da gibt es erstaunlich genaue Modelle zu und am meisten dran interessiert sind natuerlich Versicherungen.
Erstaunlicherweise fuehren die Zahlen der „Life table“ von Eurostat bis zum 35 Lebensjahr zu fast 15.000 Toten zu wenig. Das sind fast 40 %!
Genauso erstaunlich ist, dass die amerikanischen Zahlen die dtsch. Sterberaten viel besser wiedergeben. Da betraegt der aufaddierte Fehler bis zum 35. Lebensjahr nur ca. 600 Personen. Deswegen ist der folgende Graph mit den amerikanischen Zahlen erstellt worden.
Sieht erstmal nicht weiter bemerkenswert aus. Aber wenn man die Anzahl der bereits Toten aufaddiert, dann kommt man zu dem Schluss, dass die Wahrscheinlichkeit mit 64 Jahren bereits tot zu sein so grosz ist, wie die Wahrscheinlichkeit beim russischen Roulette zu sterben. Und da ich kein russisches Roulette (fuer Geld) spielen wuerde, weil mir die Wahrscheinlichkeit zu sterben zu hoch ist, ungeachtet des møglichen Gewinns, kommt dann natuerlich die Frage auf, warum man „auf die Rente sparen“ sollte. Die Aufløsung erfolgt an anderer Stelle.
Ach so, da es sich bei den berechneten Todesraten um die totalen Werte handelt, sieht es fuer Maenner (mal wieder) sogar noch schlechter aus, weil die Resilienz des starken Geschlechts gegenueber dem Tode, diese Werte zum Besseren (also kleineren Wahrscheinlichkeiten) korrigiert.
Ganz zum Schluss møchte ich dann noch auf die Daten bzgl. „Life expectancy by age, sex and educational attainment level“ hinweisen (Direktlink).
Leider gibt es da keine Daten fuer Dtschl. aber die fuer Norwegen sind drin.
Es stellt sich heraus, dass ich, als Universitaetsausgebildeter, rein statistisch gesehen in 2015 noch 48.1 Jahre vor mir hatte. Das sind 4.4 Jahre mehr, als die in 1980 geborenen, am schlechtesten gebildeten Menschen in 2015 rein statistisch noch an Jahren vor sich hatten. Bei ca. 80 Jahren Lebenserwartung, sind das ca. 5 % mehr Leben!
Das ist zwar natuerlich auch schon laenger bekannt, aber ich hatte noch nie konkrete Zahlen gesehen.
Auszerdem gibt’s dem dummen Spruch „Du lebst, aber Einstein musste sterben“ einen etwas faden Beigeschmack. Ist’s doch ein Zeichen systematischer Ungerechtigkeit … … …
Mhmmmm … møglicherweise auch nicht in allen Faellen. Wenn ’n Erwachsener meint, dass der Genuss des Rauchens fuer sie oder ihn die potenziellen Schaeden aufwiegt, dann kann ich diesem Menschen schlecht die Zigarette wegnehmen.
Das ist dann die Frage der Muendigkeit und ob „schwierige Zusammenhaenge nicht verstehen“ als Unmuendigkeit zu verstehen ist. Oft genug ist das so, siehe bspw. Kinder, Menschen mit Alzheimer, etc.
Aber es ist schon ’ne gewisse Systematik dahinter, dass weniger gebildete Menschen eher in Bedingungen leben oder arbeiten, die der Gesundheit nicht førderlich sind. Und da kann man dann natuerlich was machen … oder auch nicht … im Kapitalismus.
Aber ich schwoffte ab und nun soll Schluss damit sein. Ich dachte, dass das nur ’n kurzer Beitrag wird, aber letztlich gab es doch noch viel mehr zu entdecken, als es auf den ersten Blick schien :) .
Update: Ich stolperte ueber das Gampertz-Makeham Sterblichkeitsgesetz und dieses besagt:
Mortality rates increase exponentially with age after age 30.
.oO(Mist)