Die lange Vorrede habe ich beim letzten Mal getaetigt. Deswegen geht’s sofort los. Kurz zur Erinnerung: meine Hypothese ist, dass die Linknetzwerke (fast) aller Wikipediaseiten bei den Saisons des São Paulo FC enden. Ganz direkt geht es heute um das Folgende: Ich nehme an, dass (fast) alle Wikipediaseiten bei der 1930 Saison des São Paulo FC enden. Dann sollten die besetzten Zustaende auf den letzten Linkleveln genau der Anzahl der totalen Links dieser Seite, und der Seiten der direkt davor (bzw. zeitlich direkt dahinter) liegenden Saisons, entsprechen.
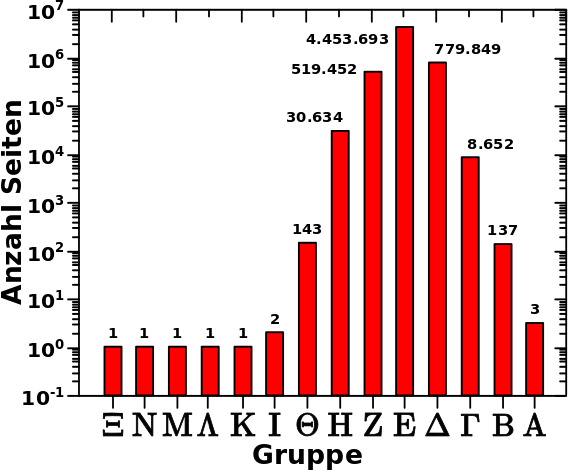
Das ist tatsaechlich das was ich sehe:
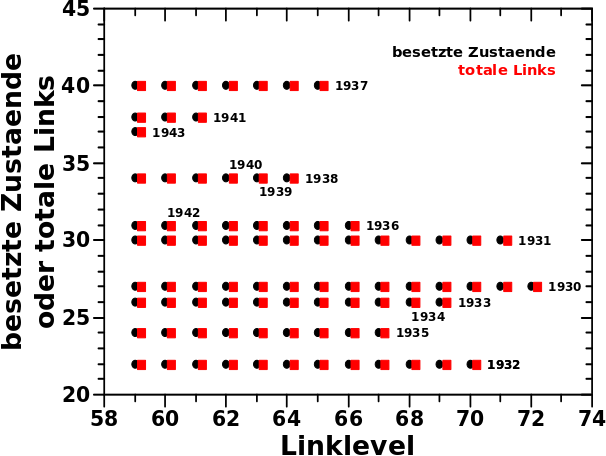
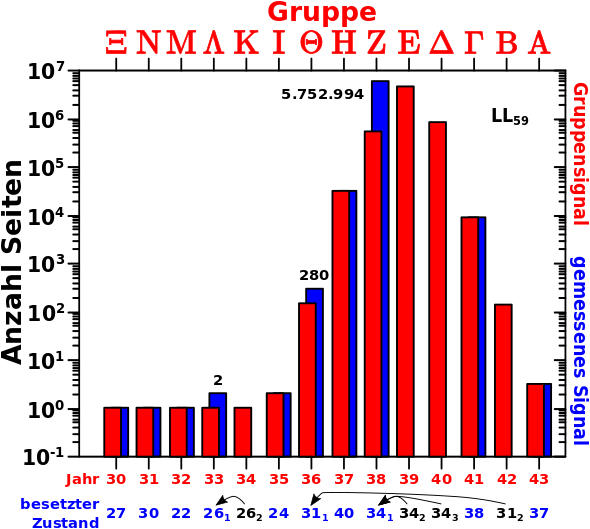
Cool wa? Aber was sehe ich hier eigentlich? Das Diagramm ist von rechts nach links zu lesen um es dann von links nach rechts zu interpretieren. Ich gehe weiter unten naeher darauf ein. Zunaechst sei so viel gesagt. Die schwarzen Punkte sind die besetzten Zustaende bei den entsprechenden Linkleveln. Die roten Punkte entsprechen der Anzahl der totalen Links einer Wikipediaseite der Saison eines gegebenen Jahres. Jede horizontale Reihe roter (!) Punkte kommt durch die totalen Links der Saison eines Jahres (manchmal mehrerer) zustande. Die entsprechenden Jahre sind gekennzeichnet, wenn sie (rueckwaerts gesehen) das erste Mal auftauchen.
Die besetzten Zustaende kann ich direkt aus den individuellen Verteilungen ablesen. Dass diese mit den roten Punkten, also der Anzahl der totalen Links der entsprechenden Seiten zum Ende der Kette der Saisons des São Paulo FC, uebereinstimmen ist ein starkes Indiz dafuer, dass meine Hypothese richtig ist.
Wenn es (scheinbar) zu keiner Aenderung im Diagramm von einem Linklevel zum vorherigen/naechsten gibt, dann liegt das daran, dass zwei hintereinander liegende Saisons die selbe Anzahl an totalen Links haben. Dann kommt natuerlich kein weiterer Punkt dazu, weil dies ein und demselben Zustand entspricht. Beispiele sind 1933 und 1934 oder 1936 und 1942.
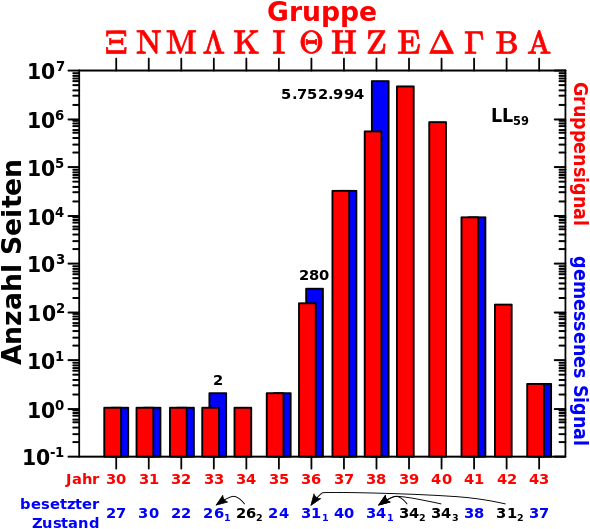
Nun naeher dazu wie das Diagramm zu lesen (und dann zu interpretieren) ist, mit Hinblick auf obige Hypothese. Zur besseren Veranschaulichung nehme man dieses Diagramm in dem ich die roten Punkte wieder weglasse, weil die ja identisch sind mit den schwarzen Punkten (den Pfeilen ist beim Lesen rueckwaerts zu folgen und beim interpretieren vorwaerts):
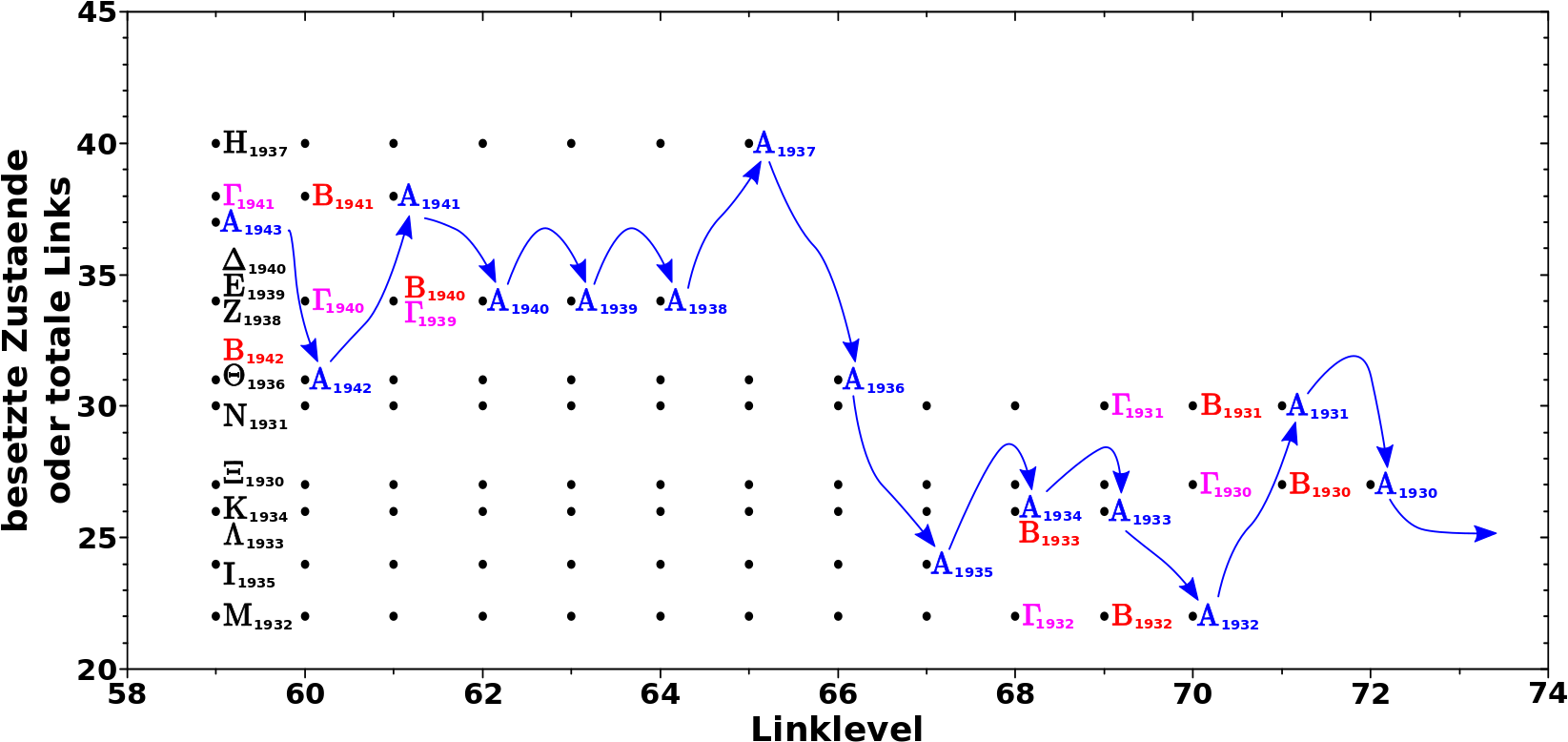
Auf LL72 sind nur zwei Zustaende besetzt — Zustand Null und Zustand 27. Letzteres bedeutet, dass die Seiten die in diesem Zustand sind, total 27 Links haben. Zustand Null wird heute nicht beachtet, denn dieser entspricht den ausgestiegenen Seiten.
Aus der Betrachtung der Aussteiger wissen wir, dass es nur (!) eine Gruppe mit drei Seiten gibt, die erst bei LL73 aussteigt und somit als einzige ein Signal auf LL72 geben kann. Ich gebe dieser Gruppe den Namen Alpha und entsprechend der Hypothese muss Gruppe Alpha sich im Jahre 1930 befinden. Das Jahr 1930 hat tatsaechlich 27 Links in meinen Daten.
Wir gehen rueckwaerts und auf LL71 sind drei Zustaende besetzt, wobei Zustand Null wieder unberuecksichtigt bleibt. Somit bleiben als besetzte Zustaende nur Zustand 27 und Zustand 30. Einer dieser Zustaende muss von Gruppe Alpha kommen. Diesmal aber aus dem Jahre 1931, welches tatsaechlich 30 totale Links in meinen Daten hat. Der andere Zustand wird durch Gruppe Beta besetzt, welche auf LL71 zum letzten Mal zum Gesamtsignal beitraegt. Entsprechend der Hypothese sollte Gruppe Beta sich auf LL71 im Jahre 1930 (und somit Zustand 27) befinden. Das ist genau das, was in den Daten zu sehen ist.
Wir gehen noch ein Linklevel rueckwarts zu LL70 und die dort besetzten Zustaende sind 27, 30 und 22. Weil wir rueckwaerts gehen wird Gruppe Gamma „wiedererweckt“ und befindet sich im Jahre 1930. Gruppe Beta ist hier nun im Jahre 1931 und Gruppe Alpha im Jahre 1932 (mit 22 totalen Links).
Der naechste Schritt rueckwaerts folgt dem gleichen Schema. Spaetere Gruppen besetzen Zustaende die (rueckwaerts gesehen!) durch Gruppe Alpha eingefuehrt wurden und Gruppe Alpha selber fuehrt via des Jahres 1933 den Zustand 26 ein.
Nun wird’s aber ein ganz klein bisschen komplizierter. Wenn Gruppe Alpha beim naechsten Rueckwaertsschritt ins Jahr 1934 springt, dann bleibt es im Zustand 26, weil dieses Jahr genausoviele totale Links hat wie 1933. Gleichzeitig besetzt nun aber auch Gruppe Beta Zustand 26 (via des Jahres 1933).
Noch einen Schritt rueckwaerts verlaeszt Gruppe Alpha Zustand 26 wieder (und geht ueber zu Zustand 24), Gruppe Beta bleibt in Zustand 26 (aber nun im Jahr 1934) und hinzu kommt in den selben Zustand Gruppe Gamma (via des Jahres 1933).
All das was ich hier niederschrieb ist im rechten Teil des obigen Diagramms entsprechend markiert.
So geht das dann weiter so weit das Diagramm reicht. Dass bei frueheren Linkleveln immer noch Signal aus Zustand 27 kommt liegt natuerlich daran, dass weitere Gruppen „wiedererweckt“ werden und die genannten Zustaende dann weiterhin besetzen.
Zu interpretieren ist das dann in der richtigen Reihenfolge, wobei „richtig“ in diesem Falle aufsteigende Linklevel meint.
Bei LL59 sind (in dieser Reihefolge) die Zustaende 27, 30, 22, 26, 26, 24, 31, 40, 34, 34, 34, 38, 31, und 37 (man beachte die Mehrfachnennungen gewisser Zustaende!) durch die Gruppen Xi, Nu, Mu, Lambda, Kappa, Iota, Theta, Eta, Zeta, Epsilon, Delta, Gamma, Beta, und Alpha besetzt, welche sich jeweils in den Jahren 1930, 1931, 1932, 1933, 1934, 1935, 1936, 1937, 1938, 1939, 1940, 1941, 1942 und 1943 befinden. … … … Ich gebe zu, dass ich das nur so weit getrieben habe, weil ich schon immer mal das Symbol fuer Xi benutzen wollte … tihihi.
Beim Schritt zu LL60 bewegen sich alle Gruppen ein Jahr rueckwaerts und in die entsprechenden Zustaende; Gruppe Alpha zu Zustand 31, Gruppe Beta zu Zustand 38, Gruppe Gamma zu Zustand 34 usw. Gruppe Xi steigt aus.
Dito beim Schritt zu LL61; Gruppe Alpha zu Zustand 38, Gruppe Beta zu Zustand 34, Gruppe Gamma (ebenso) zu Zustand 34 usw. Gruppe Nu steigt aus.
Das Beschriebene ist entsprechend im linken Teil des obigen Diagramms markiert und die geneigte Leserin oder der geneigte Leser møge den blauen Pfeilen im Diagramm (und somit Gruppe Alpha) folgen um mittels dieser Argumentation bis zum Ende zu gelangen.
Zum Abschluss sei dies gesagt: die Anzahl der totalen Links der Saisons des São Paulo FC stimmt (zum Ende des Linknetzwerkes) auf so vielen Linkleveln mit den besetzten Zustaenden ueberein, dass dies ein extrem starkes Indiz fuer die Richtigkeit der Hypothese ist.
ABER, dadurch dass ich nicht im Einzelnen nachvollziehen kann, welche Seite auf welchem Linklevel zitiert werden, kønnte es immer noch sein, dass das einfach nur Zufall ist. Oder anders: es ist møglich dass die drei Wikipediaseiten von Gruppe Alpha am Ende alle in drei verschiedenen Seiten sind, die zufaelligerweise alle 27 Links haben. Ich gebe zu, dass das aber schon ungeheure Zufaelle sein muessten, wenn das bei so vielen Linkleveln komplett uebereinstimmen soll. Die Chance dafuer ist also sehr klein, aber nicht null.
Heute habe ich mir nur die Position der besetzten Zustaende angeschaut, aber nicht wie „voll“ diese sind. Diese Information und wie sich der „Fuellstand“ „zeitlich“ entwickelt werde ich beim naechsten Mal untersuchen — Spoiler: was ich dort sehe bringt die Sicherheit fuer die Richtigkeit der Hyptohese so nahe an 100 %, dass die verbleibende potentielle Møglichkeit der Unsicherheit nicht mal mehr als „Rundungsfehler“ gelten kønnte.
Dafuer muss ich eine coole Achsentransformation durchfuehren … und um all das zu erklaeren brauche ich ein paar Wørter, aber dieser Beitrag hier ist schon so lang.