Søren in Norwegen

Aus der Entwicklung der Anzahl der Selbstreferenzen kam damals eins der schønsten Ergebnisse all dieser Untersuchungen heraus (die Verbildlichung des Sprichworts „vom Hundertsten ins Tausendste kommen“). Das muesste ich eigentlich nicht nochmal machen, denn beim letzten Mal zeigte sich ja, dass die entsprechen Daten aus 2019 und 2023 uebereinander liegen und somit die selben Anstiege haben (es wuerde also eine Art „Autoreproduktion“ vorliegen).

Besagte Anstiege wurden aus doppellogarithmischen Plots „herausgezogen“ … die waren aber (noch) nicht kumulativ, denn da bin ich erst spaeter drauf gekommen. Bei dem spaeter hatte ich das dann zwar nochmal kurz angeschaut, aber nur qualititativ (vulgo: draufgucken ob das richtig aussieht) und nicht quantitativ.

Das aendert nix daran, dass ich das nicht nochmal machen muesste … aber ich hab mir nun ein Programm geschrieben, welches kumulative log-log Diagramme automatisch erstellt und mittels linearer Regression anpasst … mit dem feinen Zusatz, dass dieses Programm erlaubt, vorne und hinten Punkte „abzuschneiden“ (weil die manchmal Aerger machen) und das dann mit den Originaldaten direkt verglichen werden kann.
Oder anders: ich hatte den kumulativen Teil vorher immer manuell gemacht und das dauert ’ne Weile wenn man das fuer viele Datensaetze machen muss. Ebenso ist es zeitaufwaendig „Aerger machende Punkte am Anfang und Ende“ zu entfernen und jedes Mal die lineare Regression durchzufuehren. Das waren die Gruende, warum ich das damals dann nur nochmal qualitativ anschaute. Aber all das ist jetzt VIIIIIIEEEEL schneller … und deswegen hab ich das jetzt doch nochmal quantitativ-isiert:

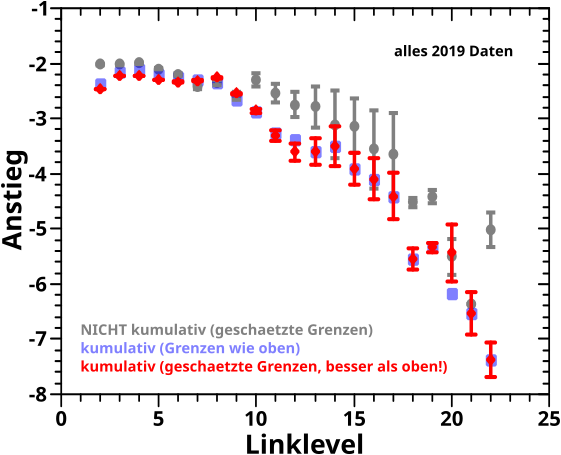
Weil die 2019 und 2023 Daten hierfuer uebereinander liegen, vergleiche ich in dem Bild natuerlich nicht die, sondern was Anderes. Naemlich die urspruenglichen Anstiege der linearen Regression, ermittelt aus NICHT kumulativen log-log Diagrammen und die Anstiege die ich mittels des besagten (kumulativen) Programms bekommen habe.

Im Wesentlichen stimmt das ueberein. Wobei ich den neuen Daten (aus kumulativen Plots) eher vertraue wuerde. Zur Erklaerung der Unterschiede kommen die Fehlerbalken und die „duennblauen“ Punkte ins Spiel. Aber der Reihe nach.

Erstens, „zappeln“ NICHT kumulierte Daten mehr. Insb. hin zu kleinen Haeufigkeiten (wenn also nur noch wenige Punkte zum Signal beitragen). Dieses „Zappeln“ fuehrt dann zu gewissen „Fehlerbalken“ und der wahre Wert des Anstiegs hat eine gewisse (meist 95 %) Chance innerhalb dieses Intervalls zu liegen. Wenn man die Fehlerbalken mit in Betracht zieht dann ueberlappt sich da schon recht viel.
Apropos Fehlerbalken; die Ergebnisse der linearen Regression von kumulativen Daten muessen korrigiert werden. Bei den Werten fuer den Anstieg muss man hier nur eine eins abziehen. Der Betrag des Anstiegs wird also grøszer. Das ist einfach. Ich weisz aber nicht, inwieweit die Fehlerbalken durch die Kumulierung beentraechtigt werden. Mein Bauchgefuehl und halbgares Verstaendniss der Mathematik sagt mir aber, dass die roten Fehlerbalken etwas (ich weisz nur nicht wieviel) laenger werden sollten … das wuerde dann zu noch mehr Uebereinstimmungen fuehren.

Damals musste ich auszerdem oft den (langen) „Schwanz“ der Daten in den NICHT kumulativen Plots abschneiden, denn ansonsten haette die lineare Regression nix Vernuenftiges errechnet. Diese „Grenzen“ fuer die Regression hatte ich mehr oder weniger mit dem Auge abgeschaetzt. Zum Glueck schrieb ich die konkreten Werte fuer besagte Grenzen auf (das wird gleich nochmal wichtig).
Auch bei kumulierten Daten muss man Punkte „aufgeben“ (siehe oben). Aber es muessen laengst nicht so viele Punkte „weggeschmissen“ werden. Meist weniger als ein Dutzend (oder sehr oft auch gar keine), wenn die Daten dann offensichtlich einem Potenzgesetz gehorchen. (Im Unterschied zu manchmal hunderten (!) bei nicht kumulativen Plots)

Nun gibt es in obigem Bild doch genuegend Abweichungen, dass mir das (mal wieder) keine Ruhe liesz und ich da genau hinschaute. Konkret „schnitt“ ich bei den kumulativen Plots genau so viele Punkte ab, wie damals bei den grauen Daten. Das spiegelt sich in den „duennblauen“ Punkten wieder (Fehlerbalken hab ich weggelassen). Und siehe da! Die stimmen im Wesentlichen mit den roten Punkten ueberein.
Das war beruhigend herauszufinden, denn damit lag der Fehler ja ganz eindeutig nicht bei mir. Vielmehr bedeutet dies, dass die Unterschiede im obigen Diagramm tatsaechlich auf die „Methode“ an sich (also NICHT kumulative log-log Plots und dem staerkeren „Herumzappeln“ dort) zurueckzufuehren sind, als auf das Abschaetzen der Grenzen fuer die lineare Regression. Oder anders: (bestimmt nicht nur) die grauen Fehlerbalken sollten vermutlich noch laenger sein.

So … wie gesagt, das hier ist keine Reproduktion im Sinne dessen, dass ich mir bzgl. der Daten aus unterschiedlichen Jahren anschaue … aber ’ne Art Reproduktion ist’s ja doch und weil ich da jetzt doch noch ein kleines Werkzeug zu programmiert und mir das alles nochmal „durchgerechnet“ hatte, wollte ich das hier auch aufgeschrieben haben.