Endlich komme ich zur Normalverteilung und wie diese …
[…] mit dem Fortschreiten der Menschheit in eine ganz wunderbare Zukunft zu tun hat.
Aber bevor ich weiterschreibe møchte ich darauf hinweisen, dass ich die Argumente ueber die ich hier schreibe von woanders (mehr oder weniger direkt aus dem dortigen Punkt 2) uebernommen habe. Natuerlich mit Modifikationen und ein paar anderen (auch weiterfuehrenden) Quellen. Ehre wem Ehre gebuehrt heiszt es ja so schøn, nicht wahr.
Ich erwaehnte letztes Mal, dass die Verteilung der Ergebnisse von Intelligenztests auf eine Normalverteilung projiziert wird mit einem Mittelwert von 100 und einer Standardabweichung von 15. Das ist also im Grenzfall unendlich vieler Menschen eine klar definierte Funktion.
Ich erwaehnte im ersten Beitrag dieser Serie, dass der Fortschritt der Menschheit (im Gegensatz zur Aufrechterhaltung des zugrundeliegenden Wohlstands!) von besonders schlauen Menschen abhaengig ist.
Da kønnte man annehmen, dass der Fortschritt schneller fortschreitet, wenn wir viel mehr wirklich schlaue Leute haben. Ob das gut oder schlecht ist, ist eine ganz andere Frage und soll hier nicht diskutiert werden … meine Meinung in ganz kurz: „JA, das ist gut, ABER …“.
Aber wie schlau ist denn eigentlich „wirklich schlau“?
Das Problem ist nun, dass spezifische, allgemein als wirklich schlau anerkannte, Individuen nicht unbedingt Intelligenztests gemacht haben. Dies gilt natuerlich insb. fuer historische Figuren, als es diese Tests noch nicht gab. Man kann das aber prinzipiell abschaetzen und hierbei kam mir ein Text zugute, auf den mich die „obskure Quelle“ vom letzten Mal aufmerksam machte. .oO(Da sieht man mal wieder, wie wichtig es ist, auch die Quellen seiner Quellen zu checken.)
Besagter Text ist: Anne Roe, The making of a scientist, Dodd, Mead & Company, 1953 … und ’ne Kopie zu finden war erstaunlich einfach und es wundert mich ueberhaupt nicht, dass es dort war (man beachte, dass das auf der selben Domain liegt, auf der obiger Artikel publiziert wurde, von dem ich die Argumente fuer diesen Beitrag hier klaute der mich zu diesem Beitrag inspirierte). Wieauchimmer, man wenn man in diesem Buch zur Tabelle auf Seite 155 (Seite 81 in der PDF-Datei) schaut, dann sieht man Abschaetzungen der IQ’s prominenter historischer Figuren.
An dieser Tabelle møchte ich besonders herausheben, dass die dort aufgefuehrten Personen ohne Zweifel als unheimlich wichtig fuer den Fortschritt der Menschheit, und damit unseren heutigen zugrundeliegenden Wohlstand, anerkannt sind.
Wenn man sich die IQ’s anschaut, dann sieht man, dass da keiner unter 160 liegt … und das ist der Wert, den ich nehme ich als Grundlage fuer die weitere Diskussion bzgl. der Anzahl „wirklich schlauer Leute“ nehme.
Wie viele sind das denn nun ganz konkret? Nun ja, ganz konkret kann das niemand sagen weil wir ja keine Messdaten haben. Und selbst wenn wir die haetten, so ist es schwierig IQ-Tests zu erstellen fuer Menschen mit besonders hohem IQ. Aber wenn wir davon ausgehen, dass die obige Definition bzgl. der Verteilung der IQ-Punkte richtig ist, dann kønnen wir das zumindest abschaetzen.
Ein Wert von 160 ist vier Standardabweichungen vom Mittelwert entfernt. Da die Funktion der Normalverteilung bekannt ist, muss man also nur das Integral von 160 bis Unendlich berechnen um den Anteil wirklich schlauer Menschen zu erhalten … super einfach wa … die Løsung des Integrals steht im Bronstein … oder auch bei der Wikipedia.
Dummerweise enthaelt die Stammfunktion die Fehlerfunktion. Diese hat einen spezifischen IQ-Wert als Argument und enthaelt dann ein weiteres Integral in welchem dieser Wert als obere Grenze des Integrals genommen wird. Immer noch erstmal easy-peasy, nicht wahr. Dummerweise ist dieses Integral (im Wesentlichen) die Fehlerfunktion selber … oder anders: die Fehlerfunktion kann nicht mittles elementaren Funktionen ausgedrueckt werden … Verdammt!
Das kann man aber (sehr genau) abschaetzen und gluecklicherweise haben andere Menschen das schon mal fuer ein paar IQ-Werte getan. Ich verlasse mich darauf und sehe, dass nur eine von 31,574 Personen einen IQ hat, der vier Standardabweichungen ueber dem Mittelwert liegt. Man beachte, dass man den dort angegebenen Wert verdoppeln muss, denn ich bin ja nur an vier Standardabweichungen UEBER dem Mittelwert intessiert.
Das ist ’ne nette Zahl, aber auch nur ’ne Obergrenze. Leider kommt hinzu, dass die Wahrscheinlichkeit fuer noch schlauere Menschen nichtlineaer abnimmt. Einen Kopernikus oder Buffon kann ich prinzipiell in Stendal finden, aber nur _einen_, nicht Beide. Fuer Kepler oder Gay-Lussac braucht es schon ein Berlin (wieder nur fuer Einen der Beiden). Und fuer Newton oder Laplace muss man dann ganz China absuchen (dito) … Und Leibniz IQ wurde mit 205 abgeschaetzt … HA! War mir schon immer klar, das Newton ein intellektuelles Leichtgewicht war im Vergleich zu Leibniz!
Das muss jetzt fuer alle Werte dazwischen gemacht werden und schwupps hat man den Anteil wirklich schlauer Menschen … … … mich duenkt ich erwaehnte bereits die Schwierigkeiten das Integral der Normalverteilung selbst fuer konkrete IQ-Werte zu løsen … *seufz*.
Gluecklicherweise ist ein anderer Weg viel einfacher: ich kann das Ganze auch einfach simulieren! Die Simulation sieht dann so aus, dass ich zufaellig IQ-Werte aus einem „Beutel“ ziehe und dann schaue wie viele davon grøszer als 160 sind. In dem „Beutel“ sind die IQ-Werte normal verteilt. Ich ziehe da also den IQ-Wert 100 am haeufigsten heraus und nach „unendlich vielen“ Ziehungen habe ich ca. 31,574 mal mehr Werte die kleiner sind als 160.
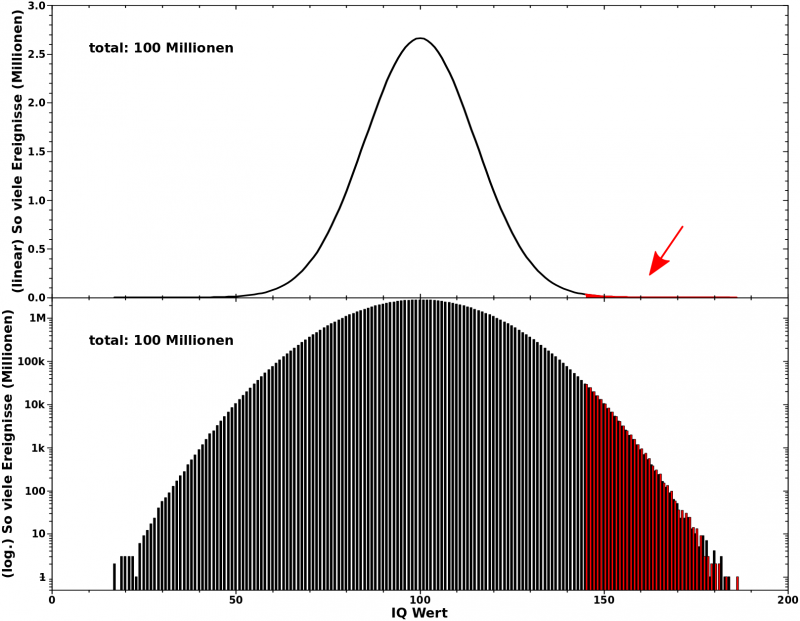
In diesem Bild versuche ich die Problemstellung nochmals im Gesamten zu veranschaulichen.
Ich habe zwei Mal jeweils 100 Millionen „Ziehungen“ aus dem „IQ-Werte-Beutel“ gemacht. Beim ersten Mal habe ich die komplette Verteilung notiert (schwarze Kurve/Balken) und beim zweiten Mal nur wenn ein Wert grøszer oder gleich 145 war (rote Kurve/Balken). Warum ich schon aber einem IQ -Wert von 145 schaue wird beim naechsten Mal klar.
Im oberen Bild, mit einer linearen Ordinate, sieht man, dass die gesamte Verteilung (schwarze Kurve) die charakteristische Glockenkurve ergibt. Man sieht auch, dass man im IQ-Bereich der hier von Interesse ist (rote, ausgefuellte Kurve) nix sieht. Die Gruende schrieb ich oben nieder.
Stellt man das Ganze mit einer logarithmischen Ordinate dar, tritt die Information die im roten Bereich liegt viel besser hervor. Es zeigt sich ganz deutlich, warum man bei einer linearen Darstellung nichts sieht, denn die Anzahl der Ziehungen mit einem IQ von 160 betraegt nicht einmal 1000.
Ich habe hier mit Absicht zwei Simulationen gemacht, um zu zeigen, dass das statistisch zwar alles ganz klar ist, aber bei realen endlichen Ereignissen Schwankungen in dem Bereich durchaus relevant sind. 100 Millionen entspricht fast der Anzahl der Menschen in Dtschl. Bei der einen Simulation habe ich aber 10 Ereignisse mit einem IQ-Wert von 175 und bei der anderen 13. Ich denke, dass es doch einen gewaltigen Unterschied macht, ob man 13 Keplers hat oder nur 10. Was natuerlich weniger an dem Unterschied von 30 % liegt, sondern an der „Gewaltigkeit“ eines Keplers.
Bei nur 100 Millionen „Ziehungen“ war dann auch noch kein Laplace dabei.
Wieauchimmer, da hier noch kein Laplace dabei war, habe ich die Simulation nochmals durchgefuehrt fuer die gesamte Menschheit … 8 Milliarden Ereignisse insgesamt … aber weil der Artikel schon so lang ist, muesst ihr, meine lieben Leserinnen und Leser, darauf bis zum naechsten Mal warten.
Leave a Reply