Søren in Norwegen

Nachdem ich beim letzten Mal das (zugegeben SEHR spezifische) Problem im Detail erklaerte, folgt heute nun die (ebenso detaillierte) Erklaerung der Løsung. Es wird also wieder technisch und kleinteilig.

Ich erwaehnte bereits, dass die …

[…] Verteilung ueber mehrere Grøszenordnungen […] mittels logarithmisch, unterschiedlich grosze Werteeimer hantiert [wird].

Und das Prinzip hatte ich damals auch schon mal erklaert und recht erfolglos angewendet. Ich habe die damalige Methode etwas modifiziert, aber der Grundgedanke bleibt der Selbe und der geht so.
Zunaechst denke man sich einen Strich auf einer einer logarithmischen Achse; bspw. bei der 20 oder der 700. Dort wird ein Werteeiner hingestellt, und alle Werte die vor diesem Strich liegen (aber HINTER dem vorherigen Strich) werden in diesen Werteeimer sortiert. Im ersten Beispiel also alle Werte von 11 bis 20, im zweiten Beispiel alle Werte von 601 bis 700 … der Wert der genau auf dem Strich liegt kommt also auch mit rein.
Weil die Werteeimer auf den Strichen einer logarithmischen Skale „gestellt“ werden, nenn ich das Grøszenordnungshistogramm.

Das beim letzten Mal besprochene Problem mit Verteilungen ueber mehrere Grøszenordnungen brachte mich schon sehr frueh auf die Idee der Grøszenordnungshistogramme … das fuehlte sich irgendwie richtig an, dass das besagte Problem damit handhabbar wird. Aber meine Werteeimer gingen ueber eine gesamte Grøszenordnung (also bspw. von 1,000,001 bis 10,000,000) und das war „zu grob“ und deswegen ging das was ich mir ausmalte nie auf.
Ich denke, das lag auch daran, dass ein Wert von bspw. 5,000,000 (die Mitte des Beispiels) im Wesentlichen genauso nahe an der 10 liegt (also sechs Werteeimer vorher), wie an der oberen Grenze des Werteeimers in dem die tatsaechliche Einsortierung dann stattfand. Und viel naeher an allen Werteeimern dazwischen. Die viel kleineren Intervalle løsen dieses Problem (was mir uebrigens schon damals „Bauchschmerzen“ bereitete) und machen die Methode damit praktikabel.
Hinzu kam auch, dass ich das nur in normalen Diagrammen verwenden wollte … was mir nicht besonders nuetzlich schien und scheint (siehe das verlinkte Beispiel); ich hatte einen passenden Anwendungsfall also noch nicht erkannt.

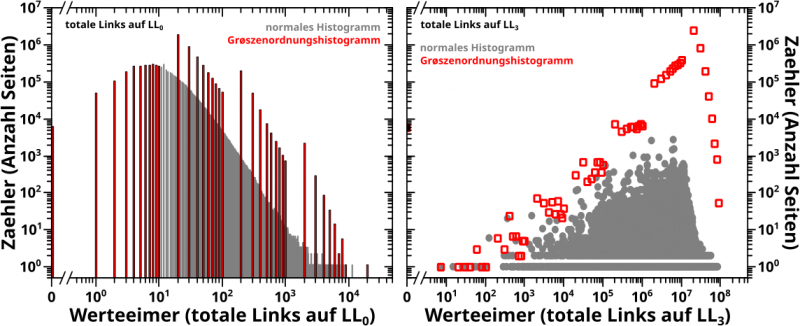
Wieauchimmer, bevor ich zu den Heatmaps komme møchte ich zunaechst auf zwei Besonderheiten von Grøszenordnunghistogrammen hinweisen, die auf die oben beschriebene Art hergestellt werden. Beide sind in diesen beiden Grafen zu sehen:

In beiden Diagrammen benutze ich Daten aus 2020. Im linken Bild sieht man die Histogramme der totalen Links auf Linklevel 0 und im rechten Bild das Gleiche, aber auf Linklevel 3. Die grauen Balken bzw. Punkte sind das normale Histogramm (kein Binning) und die roten Balken bzw. Punkte sind das Grøszenordnungshistogramm.

In Letzteren sieht man in beiden Faellen an den „Grenzen“ wo die Werteeimer pløtzlich grøszer werden „Stufen“. Das ist am leichtesten an einem Beispiel zu erklaeren.
Im Werteeimer and der Stelle 100 befinden sich maximal 10 Werte (91 bis 100). Im Werteeimer an der Stelle 200 hingegen kønnen sich bis zu 100 Werte befinden (101 bis 200), also 10 Mal mehr. Das ist hier auch tatsaechlich der Fall. Wenn nun die Anzahl der Seiten die zum Zaehler im zweiten (grøszeren) Intervall beitragen nicht schnell genug abnimmt, dann wird der entsprechende Balken im Grøszenordnungshistogramm grøszer als der davor liegende Balken, obwohl im normalen Histogramm alle Balken (im Wesentlichen) fortfahrend kleiner werden.

Wenn die Daten sich „gut“ verhalten (bspw. normalverteilt sind oder schnell genug abfallen … das kann man mathematisch sicher genau definieren), dann kann man das korrigieren. Im linken Diagramm kønnte man bspw. den Grøszenordnungshistogrammzaehler durch die Anzahl der originalen bins die in einen gegebenen Grøszenordnungseimer passen dividieren. Macht man das, so kommt die Høhe der roten Balken, denen der grauen Balken an den entsprechenden Stellen sehr nahe.
Im Allgemeinen funktioniert das aber nicht und im rechten Bild fuehrt die gleiche Methode zu grobem Unfug. Deswegen habe ich mich entschlossen die „Stufen“ einfach drin zu behalten und „anzuerkennen“. Das muss man also bei der Interpretation von Grøszenordnungshistogrammen im Hinterkopf haben.

Ein Nachteil muss das Ganze aber mitnichten sein. Diese Aussage manifestiert sich im rechten Diagramm, denn es zeigt eine Verallgemeinerung dieses Phaenomens. Dort gibt es im Grøszenordnungshistogramm nicht nur „Stufen“ an den „Grenzen“ zwischen Werteeimern unterschiedlicher Grøsze. Selbst innerhalb eines Abschnitts wo die Werteeimer alle die selbe Grøsze haben, hat die „Signalstaerke“ einen positiven Anstieg. Und das sogar obwohl im originalen Histogramm die Høhe der „Balken“ mitnichten monoton ansteigt. Ich gebe zu, dass man vermutlich etwas genau hinschauen muss um das zu sehen, insb. bzgl. der letzten Aussage. Am leichtesten ist es im Abschnitt von 10⁶ bis 10⁷ zu erkennen.
Aber genau darin liegt auch der Grund, warum das beschriebene Phaenomen kein Nachteil sein muss. Wie gesagt, kommt die „Erhøhung“ des „Signals“ im Grøszenordnungshistogramm dadurch zustande, dass da „mehr Zeuch“ in die Werteeimer „geschmissen“ wird. Im normalen Histogramm sieht man aber nicht, dass da mehr „Zeuch“ in dem Abschnitt liegt — die Punkte sind da so dicht, dass dort zum Teil buchstaeblich Millionen von Datenpunkten uebereinander liegen und damit ununterscheidbar werden. Das ist also ein „man-sieht-den-Wald-vor-lauter-Baeumen-nicht“ Problem … bzw. habe ich das an anderen Stellen als „logarithmische Komprimierung“ bezeichnet.
Beim Vergleich der unterschiedlichen Histogramme muss man aber fuer den Anstieg (bzw. die „Stufen“) im Grøszenordnungshistogramm eine Erklaerung finden … und damit wird man automatisch darauf aufmerksam, dass es da noch urst viel „Zeuch“ geben muss, was man so im normalen Histogramm nicht sieht. Natuerlich muss man auch das bei der Interpretation im Hinterkopf behalten.

Soweit dazu, der Rest geht nun ganz schnell.

Die obigen Bilder sind immer noch normale, doppellogarithmische Diagramme. Den Werteeimern wird (mindestens unbewusst) ein numerischer Wert zugeordnet. Deswegen entgehen wir auch im Grøszenordnungshistogramm nicht dem Fakt, dass die Werteeimer unterschiedliche Abstande voneinander haben. Letzteres wuerde (immer noch) zu unterschiedlich groszen Pixeln in einer Heatmap fuehren.
Nun schrieb ich aber nicht umsonst immer „Werteeimer“, denn ich will die „numerische Interpretation“ „wegabstrahieren“.
In aller Kuerze: fuer die Heatmap tue ich so, als ob die Werteeimer alle gleich grosz sind und schiebe die dann dicht an dicht. Dadurch werden alle Pixel gleich grosz.
Auch hier muss man bei der Interpretation einer solchen Heatmap im Hinterkopf behalten, dass die Werteeimer selbstverstaendlich (auch) eine „numerische Interpretation“ haben, somit auf der entsprechenden Skala natuerlich NICHT den gleichen Abstand haben und auch nicht alle gleich grosz sind. Aber wenn man erstmal so weit gekommen ist und alles bis hierher verstanden hat, dann sollte das kein Problem sein.

Und damit bin ich fertig fuer heute. Beim naechsten Mal dann endlich die Anwendung dieser Methode