Søren in Norwegen

Zur Simulation der Selbstreferenzen via „atomistischer Naeherung“ (die ich an sich eigtl. nicht nochmal machen will, weil ich das Gefuehl hatte, dass das nicht viel gebracht hat) benøtigte ich auch die Abhaengigkeit der Anzahl der Selbstreferenzen die eine Seite auf einem gegebenen Linklevel hat, von der Anzahl der Selbstreferenzen dieser Seite auf dem vorherigen Linklevel. Oder anders und an einem konkreten Beispiel: hat eine Seite mit vielen Selbstreferenzen auf LL₅ auch viele Selbstreferenzen auf LL₆?

Nachdem ich das „Konzept“ „entwickelt“ hatte, wandte ich das dann auch auf  die totalen und neuen Links und die Linkfrequenz an. Viel ist dabei nicht rumgekommen … aber ich habe den Code dafuer neu geschrieben und deshalb liegen die Ergebnisse jetzt auch fuer die 2023 Daten vor.
Hinzu kommt, dass ich fuer’s letzte und vorletzte Mal ein Werkzeug schrieb, mit welchem ich ([deutlich mehr als] halb-)automatisiert Diagramme erstellen und schøn machen kann. Anstatt also nur ein paar repraesentative Beispiele zu zeigen, kann ich nun ohne all zu viel arbeite ALLES diagrammisieren … was in diesem Falle hiesz, deutlich ueber 200 Bilder zu erstellen. Zugegeben, die meisten davon sind nur „Zwischenschritte“ im automatischen Prozess und nicht direkt im Endergebnis zu sehen … aber erstellt werden mussten die trotzdem. Das Endergebnis sind dann nur vier bewegte Bilder; eins pro Messgrøsze. Die enthalten jeweils zwei Diagramme („Rohdaten“ und Durschnittswerte … macht schonmal acht Diagramme) und laufen ueber jedes Linklevel. Bei ungefaehr 80 zu zeigenden Linkleveln macht das ueber 600 Bilder die ihr, meine lieben Leserinnen und Leser gleich sehen werdet.

Ich schreibe das hier nochmal ausfuehrlich, weil es so ein schønes Beispiel fuer einen wichtigen Teil des wissenschaftlichen Prozesses ist: hier habe ich keine „neue“ Methode entwickelt, sondern ein effektives Werkzeug geschaffen, mit dem man viel mehr abstrakte Daten (in der Form langer Zahlenreihen) in verstaendlichere Information (in Form von „bewegten“ Diagrammen) bringen kann. Das aendert nichts an den urspruenglichen Schlussfolgerungen und Ergebnissen, erøffnet aber die „Dynamik“ eines Systems im Detail zu untersuchen … was ich aber nicht mehr machen werden.

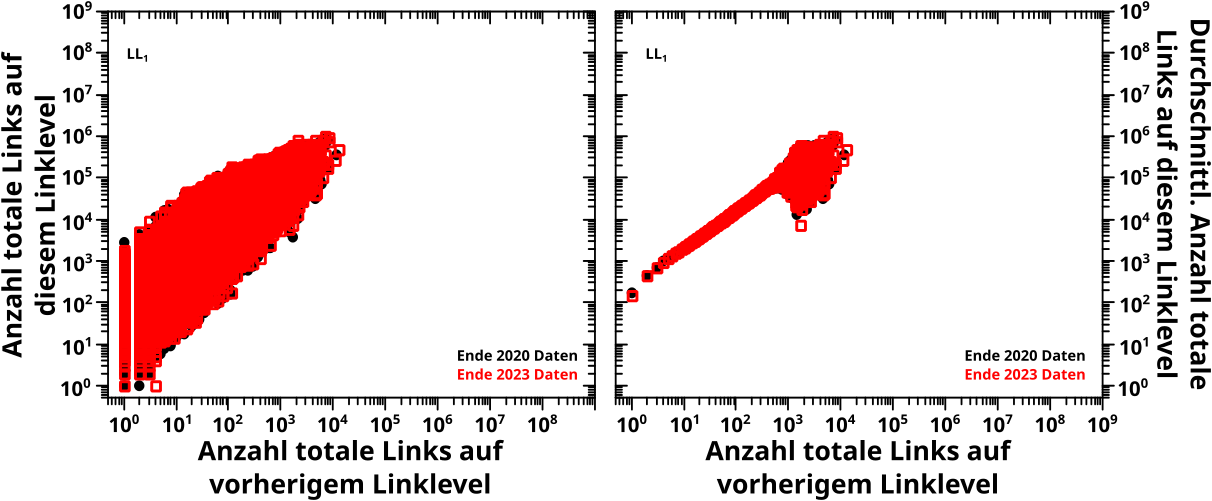
Damit genug der langen Vorrede. Hier ist die Entwicklung der totalen Links auf einem gegebenen Linklevel in Abhaengigkeit der totalen Links auf dem vorherigen Linklevel dargestellt:

Im linken Diagramm sind die „Rohdaten“ zu sehen. Im Wesentlichen entspricht jeder Punkt einer Seite … und hier geht’s auch schon los. Nicht nur wird einem gegebenen Wert auf der Abzsisse oft mehr als einen Wert auf der Ordinate zugeordnet. Viele (in spaeteren Linkleveln alle) zu sehende Datenpunkte sind „degeneriert“. Das heiszt, dass mehrere (viele) Seiten das selbe (Anzahl-Links-auf-LL_i-1, Anzahl-Links-auf-LL_i)-Paar haben. Ich komme darauf gleich nochmal zurueck.

Desweiteren ist zu sagen, dass ich alle „Nullwerte“ weglasse. Also alle Daten die entweder keine (in diesem Fall) Links auf diesem oder dem vorherigen Level hatten. Ersters entspricht einem „Nullwert“ auf der Abzsisse, Letzteres einem „Nullwert“ auf der Ordinate. Bei den totalen Links kann Letzteres nur in der Form einer „Doppelnull“ auftreten (deswegen ist das allerletzte Diagramm auf LL₈₄ leer), aber bei den Selbstreferenzen weiter unten sind beide Faelle møglich.
Ich habe mich zu diesem Schritt aus der Not heraus entschlossen, denn die Nullen bei logarithmischen Achsen mit reinzubringen ist in der Kombination meines Diagrammerstell- und Diagrammschønmachprogramms ziemlich umstaendlich. Das ist der wirkliche Grund. Ich kønnte natuerlich auch darauf zeigen, dass die Achsen bei einem Wert von jeweils 0.5 aufhøren und ein Wert von Null darunter liegt … aber das hat mich frueher ja auch nicht gestørt … als noch keine drei Grøszenordnungen weniger Diagramme zu erstellen waren.

Beim rechten Diagramm sieht man den Durchschnittswert der totalen Links zu einem gegebenen Wert auf der Abzisse. Ein Beispiel: die (totalen) Links ALLER Seiten die auf LL₂₃ fuenf Links haben werden aufsummiert und das wird durch die Anzahl dieser Seiten dividiert. Die dabei entstehende Zahl wird im Diagramm fuer LL₂₄ genommen und auf der Abzsisse ueber dem Wert fuenf als Punkt dargestellt. Wichtig: auch die „Nullwerte“ zaehlen dazu, zwar nicht wenn die Summe gebildet wird (plus Null macht ja nix) aber sehr wohl bei der Anzahl der Seiten durch die dividiert werden muss.

Das Feine ist nun, dass damit (zwangslaeufig) jedem Wert auf der Abzsisse nur ein Wert auf der Ordinate zugeordnet wird. Auszerdem gibt es (zwanslaeufig) auch keine „degenerierten“ Punkte mehr im Diagramm.

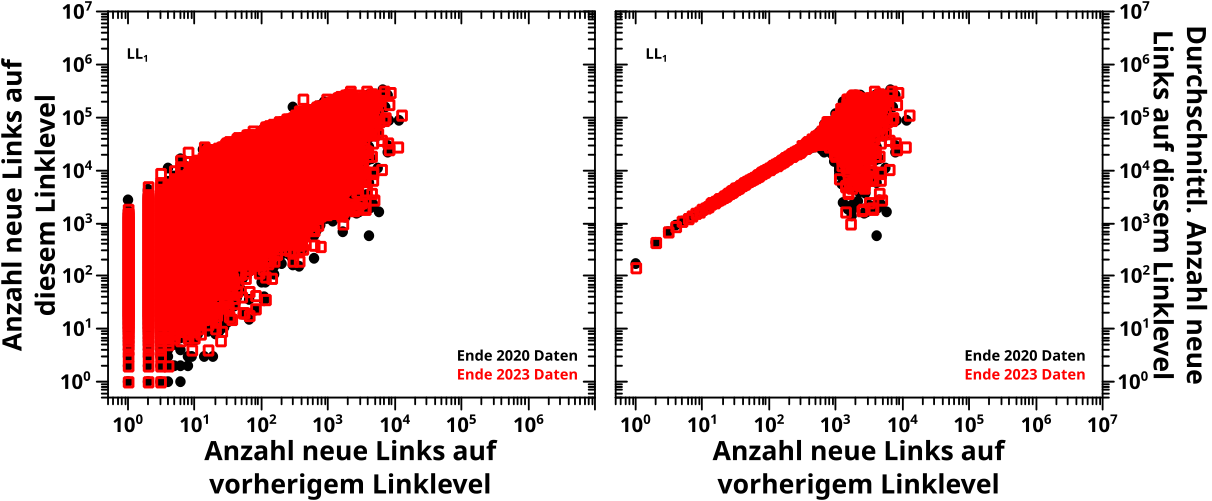
Als naechstes das gleiche fuer die Anzahl der neuen Links:

Die Achsen reichen nicht so lang (war zu erwarten) und zum Ende hin Ende zappelts nicht mehr so doll, ja steht gar still (war auch zu erwarten, wg. der „Ketten“). Kurios ist die „Verzweigung“ zwischen LL₇ und LL₁₀. Ich weise da aber nur drauf hin, ich habe das nicht weiter untersucht und werde es auch nicht tun. Das ist aber ein schønes Beispiel fuer den oben erwaehnten Prozess, dass man mittels neuer Werkzeuge (bspw.) die „Dynamik“ eines Systems besser untersuchen kann. Das ist beim Zeigen repraesentativer Datensaetze nicht aufgetaucht (denn es ist definitiv nicht repraesentativ), aber gleichzeitig aendert es auch nichts an den wesentlichen Aussagen.

Wieder gilt: die 2023-Daten reproduzieren die 2019-Daten gut.

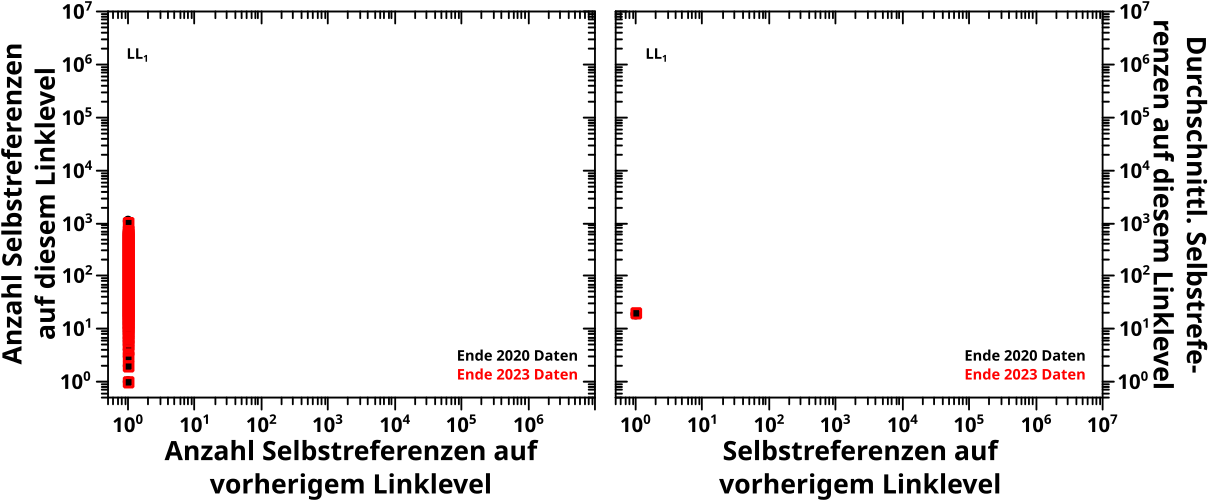
Auf zu den Selbstreferenzen:

Hier wird im rechten Diagramm wichtig, was ich oben zu den „Nullwerten“ sagte … und dass die Grenze eigtl. schon bei 0.5 liegt. Denn hier sieht man øfter Punkte die gerade so ueber der Abzsisse „herumduempeln“, weil die einem Durchschnittswert von gerade mal ein kleines bisschen ueber 0.5 Selbstreferenzen entsprechen. Man sieht nicht, dass manchmal einige Punkte auch unter dem Wert von 0.5 liegen … denn die werden ja „unterdrueckt“.
Oben bei den neuen Links sieht man aber einen Hinweis auf die unterdrueckten Punkte „indirekt“, wenn man ganz schnell hinschaut. Denn das LL₈₀ Durchschnittsdiagramm ist leer (die Rohdaten sind aber noch zu sehen); das erklaert sich natuerlich aus dem eben Gesagten.

Mehr gibt’s nicht zu sagen … ach doch: und nocheinmal reproduzieren die 2023-Daten die 2019-Daten gut.

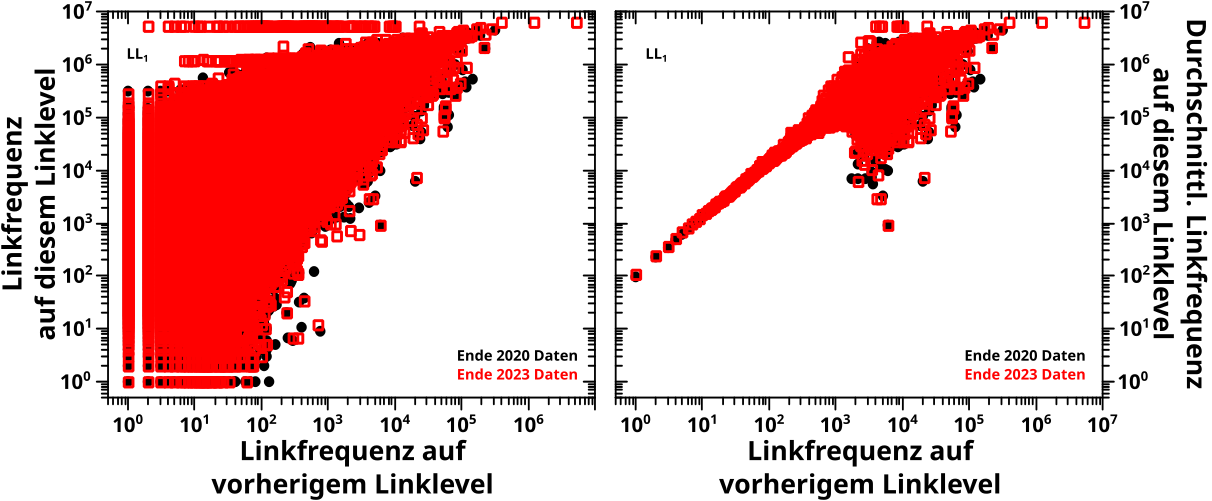
Als Letztes dann die Linkfrequenz:

Auch wenn ab ca. LL₁₅ deutlicher als bei den anderen Diagrammen zu sehen ist, dass die schwarzen und roten Punkte nicht mehr (beinahe) deckungsgleich sind, so bleiben alle Merkmale (Form, Verlauf und „Merkwuerdigkeiten“) erhalten. Deswegen bleibt mir nix weiter als zu sagen: auch hier ist die Reproduktion der 2019-Daten in den 2023-Daten gelungen.

Ach doch, eine Sache noch: waehrend der Durchschnittswert fuer die Links und Selbstreferenzen durchaus sinnvoll ist, gilt das fuer die Linkfrequenz mitnichten. Da kommt einfach keine (mehr oder weniger) gerade Linie bei raus, sondern die Ellipse bleibt bestehen. Man muss also immer die Sinnhaftigkeit und Interpretation der angewandten (nicht notwendigerweise nur mathematischen) „Umformungen“ der Daten gut durchdenken, damit man keinen Mist publiziert.

Und damit soll’s gut sein damit. Etwas wehmuetig habe ich das alles in nur einen Beitrag gepackt. Wehmuetig deswegen, weil trotz der (mehr oder weniger) automatisierten Bilderstellung, es noch fast ’ne Woche dauerte bis die hier zu sehenden Endresultate fertig waren … und die ganze Arbeit ist mit nur einem Beitrag „abgegessen“ … Uff! … Aber letztlich gibt’s nicht wirklich viel mehr dazu zu sagen und das ist auch gut so, denn um es muss noch mehr reproduziert werden … und ich will wirklich auch mal mit dem ganzen Projekt abschlieszen.

Ich gebe zu, dass ich mich davor gedrueckt habe, diesen „Revisited“-Neitrag zu schreiben … aus mehreren Gruenden.

Der Hauptgrund: Witchblade ist ein typisches Image Comic (eigtl. Top Cow, aber das ist ja nur ein Image Imprint) aus der Mitte der 90’er Jahre des letzen Jahrhunderts ist. Oder anders: leichtbekleidete Damen (und manchmal auch Herren), mit unrealistischen Kørperproportionen. Aber anstatt vieler Worte lasse ich gleich mal das Cover der 2. US-Ausgabe fuer sich sprechen:

Der Hintergrund ist natuerlich „Sex sells„, insb. dann, wenn die Leserschaft vor allem jungendliche Maenner sind. Der ich ja nunmal war Mitte der 90’er und Anfang der Nullerjahre. Ich habe mich dann entschieden das einzugestehen und nicht unter den Teppich zu kehren. Die Cover sind ein Teil der (Comic)Geschichte (und somit auch meiner) und wir schauen uns im Louvre ja auch die Akte alter Meister an. Das heiszt natuerlich nicht, dass ich das immer noch so sehe!

Desweiteren war Witchblade auch mein Lieblingscomic. Zu groszen Teilen aus obigen Gruenden, aber nicht nur, denn irgendwie steckte auch in der Geschichte viel mehr Potential als ich sonst in Comics realisiert sah. Damals haette ich das sicherlich nicht so ausgedrueckt. Nun habe ich aber innerhalb relativ kurzer Zeit einen betraechtlichen Teil meiner Sammlung nochmals gelesen. Das hat mir einen guten Ueberblick ueber die erfolgreichen (mehr oder weniger) US Superheldencomics dieser Jahre gegeben und deswegen kann ich da jetzt „den Finger draufpacken“. Leider hat sich das relativ schnell ins Gegenteil verkehrt … *seufz*.

Die interessanten Handlungsstraenge wurden relativ schnell mehr und mehr in die Laenge gezogen und mit mehr oder weniger (oft weniger) interessanten „Detektivgeschichten“ „verduennt“. Wichtige Handlungen wurden in anderen Comics (also NICHT Witchblade) weiter erzaehlt, erweitert oder zum Ende gebracht. Es half auch nicht gerade, dass mindestens eine wirklich wichtige Hauptfigur „off screen“ (also in ’ner anderen Serie) abgemurkst wurde. Der tauchte dann halt nie wieder auf und ich fragte mich was aus dem wurde.

Aber da war ja immer noch Sara Pezzini …

… die Traegerin der Witchblade in unserer Zeit. Nicht nur sah sie nett aus, sondern die Charakterentwicklung haette durchaus interessant werden kønnen. Selbst wenn’s am Ende nur ’ne typische „widerwillige Heldengeschichte“ geworden waere. Leider wurde auch das in den Sand gesetzt. Zweifel sind gut fuer die besagte Charakterentwicklung … aber nicht wenn Sara jetzt schon seit Jahren all diese mystisch komischen Sachen sieht und die Witchblade traegt.
Noch viel schlimmer: sie ist ’ne coole Heldin! Die Schreiber nehmen ihr aber immer und immer wieder die „Butter vom Brot“ und machen sie dann eher zu einer „Jungfrau in Nøten“ die gerettet werden muss, als die Traegerin einer maechtigen Zauberwaffe … schade eigentlich.

Irgendwann hab ich’s nicht mehr ausgehalten. Ich sagte mir dann: ich schau’s mir noch bis zur Jubilaeumsausgabe #50 an … zumal in Dtschl. da dann immer schon ein neues Kreativteam angepriesen wurde. Ich gebe zu, Letzteres hat tatsaechlich wieder etwas mehr Qualitaet in die Serie gebracht … aber nicht viel … und als dann auch #51 …

… nicht besser wurde, bin ich schweren Herzens ausgestiegen. Wobei „schweren Herzens“ das nur zur Haelfte beschreibt; ich hing (sicher vor allem aus nostalgischen Gruenden) an Witchblade. Die andere Haelfte war dann Erleichterung (dass es nicht besser wurde) denn zu dem Zeitpunkt war das „Loslassen“ eigtl. nur noch eine „Formalitaet“, weil besagtes Herz zu dem Zeitpunkt schon seit deutlich laengerer Zeit nicht mehr wirklich an Witchblade hing.

Eine Sache sei noch gesagt: Witchblade ist die einzige Serie, bei der irgendwie alles an einem einzigen Zeichner hing. Dies war Michael Turner (bis auf das Letzte, sind alle hier gezeigten Cover von ihm) und er war auch Co-Creator. Was den „Niedergang“ der Serie erklaert, nachdem er ging. Es ging dann zwar noch weiter bis #185, aber dazu kann ich nix mehr sagen … ich kønnte natuerlich Vermutungen anstellen, insb. unter dem Gesichtspunkt, dass nicht mal comics.org detaillierte Informationen fuer (mehr als) die letzten 50 Ausgaben hat … aber das spare ich mir.

Pøøøh … nun hab ich den Beitrag hier auch endlich mal geschrieben … mit dem Witchblade-Universum sind wir aber laengst noch noch fertig. Aber dazu ein andermal.

Aus der Entwicklung der Anzahl der Selbstreferenzen kam damals eins der schønsten Ergebnisse all dieser Untersuchungen heraus (die Verbildlichung des Sprichworts „vom Hundertsten ins Tausendste kommen“). Das muesste ich eigentlich nicht nochmal machen, denn beim letzten Mal zeigte sich ja, dass die entsprechen Daten aus 2019 und 2023 uebereinander liegen und somit die selben Anstiege haben (es wuerde also eine Art „Autoreproduktion“ vorliegen).

Besagte Anstiege wurden aus doppellogarithmischen Plots „herausgezogen“ … die waren aber (noch) nicht kumulativ, denn da bin ich erst spaeter drauf gekommen. Bei dem spaeter hatte ich das dann zwar nochmal kurz angeschaut, aber nur qualititativ (vulgo: draufgucken ob das richtig aussieht) und nicht quantitativ.

Das aendert nix daran, dass ich das nicht nochmal machen muesste … aber ich hab mir nun ein Programm geschrieben, welches kumulative log-log Diagramme automatisch erstellt und mittels linearer Regression anpasst … mit dem feinen Zusatz, dass dieses Programm erlaubt, vorne und hinten Punkte „abzuschneiden“ (weil die manchmal Aerger machen) und das dann mit den Originaldaten direkt verglichen werden kann.
Oder anders: ich hatte den kumulativen Teil vorher immer manuell gemacht und das dauert ’ne Weile wenn man das fuer viele Datensaetze machen muss. Ebenso ist es zeitaufwaendig „Aerger machende Punkte am Anfang und Ende“ zu entfernen und jedes Mal die lineare Regression durchzufuehren. Das waren die Gruende, warum ich das damals dann nur nochmal qualitativ anschaute. Aber all das ist jetzt VIIIIIIEEEEL schneller … und deswegen hab ich das jetzt doch nochmal quantitativ-isiert:

Weil die 2019 und 2023 Daten hierfuer uebereinander liegen, vergleiche ich in dem Bild natuerlich nicht die, sondern was Anderes. Naemlich die urspruenglichen Anstiege der linearen Regression, ermittelt aus NICHT kumulativen log-log Diagrammen und die Anstiege die ich mittels des besagten (kumulativen) Programms bekommen habe.

Im Wesentlichen stimmt das ueberein. Wobei ich den neuen Daten (aus kumulativen Plots) eher vertraue wuerde. Zur Erklaerung der Unterschiede kommen die Fehlerbalken und die „duennblauen“ Punkte ins Spiel. Aber der Reihe nach.

Erstens, „zappeln“ NICHT kumulierte Daten mehr. Insb. hin zu kleinen Haeufigkeiten (wenn also nur noch wenige Punkte zum Signal beitragen). Dieses „Zappeln“ fuehrt dann zu gewissen „Fehlerbalken“ und der wahre Wert des Anstiegs hat eine gewisse (meist 95 %) Chance innerhalb dieses Intervalls zu liegen. Wenn man die Fehlerbalken mit in Betracht zieht dann ueberlappt sich da schon recht viel.
Apropos Fehlerbalken; die Ergebnisse der linearen Regression von kumulativen Daten muessen korrigiert werden. Bei den Werten fuer den Anstieg muss man hier nur eine eins abziehen. Der Betrag des Anstiegs wird also grøszer. Das ist einfach. Ich weisz aber nicht, inwieweit die Fehlerbalken durch die Kumulierung beentraechtigt werden. Mein Bauchgefuehl und halbgares Verstaendniss der Mathematik sagt mir aber, dass die roten Fehlerbalken etwas (ich weisz nur nicht wieviel) laenger werden sollten … das wuerde dann zu noch mehr Uebereinstimmungen fuehren.

Damals musste ich auszerdem oft den (langen) „Schwanz“ der Daten in den NICHT kumulativen Plots abschneiden, denn ansonsten haette die lineare Regression nix Vernuenftiges errechnet. Diese „Grenzen“ fuer die Regression hatte ich mehr oder weniger mit dem Auge abgeschaetzt. Zum Glueck schrieb ich die konkreten Werte fuer besagte Grenzen auf (das wird gleich nochmal wichtig).
Auch bei kumulierten Daten muss man Punkte „aufgeben“ (siehe oben). Aber es muessen laengst nicht so viele Punkte „weggeschmissen“ werden. Meist weniger als ein Dutzend (oder sehr oft auch gar keine), wenn die Daten dann offensichtlich einem Potenzgesetz gehorchen. (Im Unterschied zu manchmal hunderten (!) bei nicht kumulativen Plots)

Nun gibt es in obigem Bild doch genuegend Abweichungen, dass mir das (mal wieder) keine Ruhe liesz und ich da genau hinschaute. Konkret „schnitt“ ich bei den kumulativen Plots genau so viele Punkte ab, wie damals bei den grauen Daten. Das spiegelt sich in den „duennblauen“ Punkten wieder (Fehlerbalken hab ich weggelassen). Und siehe da! Die stimmen im Wesentlichen mit den roten Punkten ueberein.
Das war beruhigend herauszufinden, denn damit lag der Fehler ja ganz eindeutig nicht bei mir. Vielmehr bedeutet dies, dass die Unterschiede im obigen Diagramm tatsaechlich auf die „Methode“ an sich (also NICHT kumulative log-log Plots und dem staerkeren „Herumzappeln“ dort) zurueckzufuehren sind, als auf das Abschaetzen der Grenzen fuer die lineare Regression. Oder anders: (bestimmt nicht nur) die grauen Fehlerbalken sollten vermutlich noch laenger sein.

So … wie gesagt, das hier ist keine Reproduktion im Sinne dessen, dass ich mir bzgl. der Daten aus unterschiedlichen Jahren anschaue … aber ’ne Art Reproduktion ist’s ja doch und weil ich da jetzt doch noch ein kleines Werkzeug zu programmiert und mir das alles nochmal „durchgerechnet“ hatte, wollte ich das hier auch aufgeschrieben haben.

Nun war ich schon zum zweiten Mal im Land der aufgehenden Sonne und ich bin hier noch nicht mal mit den Kuriositaeten meines ersten Besuches fertig. Was auch zeigt, dass ich schneller wieder dort war als urspruenglich angenommen :).

Wieauchimmer, als ich 2023 in Kagoshima an diesem Firmenschild …

… vorbei lief, konnte ich natuerlich nicht widerstehen und musste das fuer euch, meine lieben Leserinnen und Leser, dokumentieren.
Find ich gut, dass die so ehrlich sind, da weisz man, welchen Telefonservice man lieber vermeiden sollte :).

Das ist uebrigens keine Uebersetzung der Schriftzeichen darunter:

Vielmehr duenkt mich, dass das deren Firmenmotto ist … das ist: witzig.