Ich schreibe diesen Beitrag etliche Wochen vor meiner Reise in den fernen Osten. In der Woche bevor dieser Artikel hier erscheint bin ich nach Plan schon zurueck. Von eurer Warte, meine lieben Leserinnen und Leser, dehnte die Sommerpause sich um eben diese Woche aus weil … øhm … ich nehme an, dass ich da noch halb im Jetlag bin (auch wenn der eigtl. in die richtige Richtung geht beim Rueckflug) … und auszerdem ist’s im Sommer warm und bei høherer Temperatur dehnt sich i.A. alles aus (also auch die Sommerpause).
Aber nun geht’s weiter und zwar mit dem was ich damals als Aussteiger bezeichnete. Oder anders: ich schaute (damals) wieviele Seiten ab welchem Linklevel keine totalen Links mehr haben. Konzeptionell ist diese Herangehsensweise etwas „haarig“, denn bei den Selbstreferenzen kønnen Seiten „mittendrin“ keine Selbstreferenzen mehr haben, aber zu einem spaeteren Linklevel dann doch wieder. Das habe ich in einem anderen Zusammenhang als „Reaktivierungen“ bezeichnet und diesen Aspekt lasse ich heute zunaechst auszen vor.
Um dieser „Haarigkeit“ zu entkommen, drehte ich bei der Neuprogrammierung des hierzu gehørigen Analyseprogramms den Ansatz einfach um: ich schaue von hinten, ab welchen Linklevel eine Grøsze von Interesse einen Wert UNGLEICH Null hat. Das ist im Wesentlichen das Gleiche, mit dem kleinen Unterschied, dass alle Grafen hier um eins nach Links verschoben sind, denn der letzte Wert ungleich Null kommt ja genau ein Linklevel vor dem ersten Nullwert (mit der Ausnahme der Selbstreferenzen).
Das war alles was ich damals machte. Aber schon bei den Maximumspositionen, „sehe“ ich auch hier nicht mehr nur die Position des Ausgangs, sondern auch den Wert (einer gegebenen Grøsze von Interesse), den die Seiten am Ausgang haben. Anders als beim letzten Mal (wo ich diese neue Sache erst einfuehrte), mache ich da nicht mehrere Artikel draus, sondern handle das heute alles auf einmal ab.
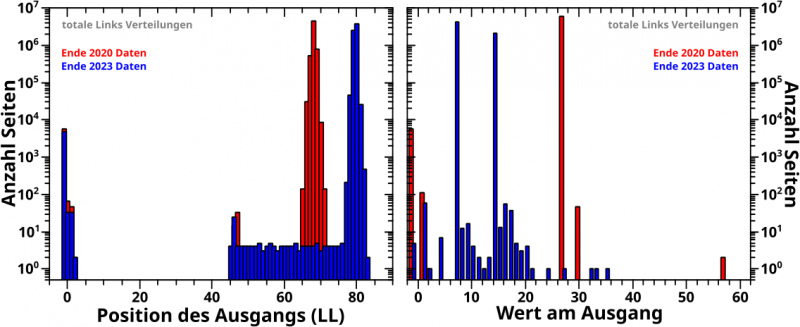
Und jetzt geht’s los, wie so oft, zunaechst mit den totalen Links:
Aha! Bzgl. der Position des Ausgangs (linkes Diagramm), reproduzieren die 2023 Daten die Form der Verteilung der 2020 Daten. Ein paar Balken am Anfang mit ungefaehr gleicher Høhe, dann erstmal nix, dann ein „Wald“ mit kurzen Balken und am Ende ein hoher „Berg“ (auch mit ungefaehr gleich hohen Balken). Letzteres bedeutet, dass alle Seiten ungefaehr zum gleichen Zeitpunkt aussteigen und war der erste Hinweis auf Ketten (oder „Familien“) von Seiten (damals dauerte es noch eine Weile, bis ich das in einem anderen Zusammenhang erkannte). Oder anders: Reproduktion gelungen.
In den 2023 Daten scheint es mindestens eine Kette zu geben, die 10 Linklevel laenger ist, als die laengste Kette in den 2020 Daten. Da dies aber keine „kollektive Eigenschaft“ ist, die man ueber alle Seiten „mitteln“ kann, sondern aus dem Verhalten individueller Seiten folgt ist das jetzt nicht verwunderlich, dass das nicht reproduziert wird. Ich komme da vllt. spaeter nochmal drauf zurueck, falls ich mir die Ketten nochmal anschaue … weisz ich jetzt aber noch nicht.
Ach ja Mensch! Jetzt hab ich vergessen zu sagen, dass bzgl. des am weitesten links liegenden Balkens (bei einem Wert auf der Ordinate von minus eins) das Selbe gilt wie bei den Maximapositionen: dieser Balken ist „flachen“ Verteilungen zuzuordnen! Zu Details lese man den oben verlinkten entsprechenden Beitrag.
Weiter nun mit dem Diagramm auf der rechten Seite – der Anzahl der totalen Links am Ausgang … also der Ausgangswert … was natuerlich nicht hinhaut, weil ein Ausgangswert eigtl. meist der allererste Wert ist, von dem alles aus geht. Wieauchimmer, das wird nun scheinbar (!) ueberhaupt nicht reproduziert und das wundert mich gar nicht. Das haette nur dann (mehr oder weniger) direkt (!) reproduziert werden kønnen, wenn es keine laengere Kette als damals gaebe. Die Seiten der neuen Kette haben natuerlich eine ganz andere Anzahl an Links.
Interessant sind zwei Sachen in den 2023 Daten. Zum Einen hat die Verteilung mehr Balken. Es gibt also mehr Seiten die als Ausgang fungieren als bei den 2020 Daten. Wenn man drueber nachdenkt war das durchaus zu erwarten und die Anzahl der Balken ist jetzt zwar ’ne halbe Grøszenordnung mehr, aber das liegt vor allem daran, weil die 2020 Verteilung so wenige Balken hat. Waere letzte doppelt so grosz, dann haette man nur einen Unterschied von ca. einem Faktor 2 und das wuerde nicht verwundern.
Die zweite Sache ist da schon deutlich interessanter, denn es gibt in den 2023 Daten ZWEI sehr hohe Balken mit ca. 4 Millionen und ca. 2 Millionen Seiten die dort aussteigen. Das kønnte ein Hinweis sein, dass es ZWEI Ketten mit … mhmmmm … ich denke der selben Laenge gibt (oder vielleicht plusminus eins) und ca. 1/3 aller Seiten landen etwas frueher in Kette #1 (und sind mit der etwas frueher fertig), waehrend die anderen 2/3 Kette #2 etwas frueher abarbeiten um dann zuletzt in Kette #1 zu sein und mit der abzuschlieszen.
Das kønnte man mal naeher untersuchen … und wie oben erwaehnt, das mache in diesem Falle sogar ich, falls ich mich den Ketten nochmals zuwende.
Festzuhalten bzgl. des rechten Diagramms ist das Folgende: in den den individuellen Eigenschaften wird der Wert am Ausgang NICHT reproduziert, aber bzgl. der _kollektiven_ Eigenschaften dann doch. Es gibt keine Seiten die massenhaft Links am Ausgang haben; alles tuemmelts sich um ca. den Wert 15 auf der Ordinate. Und auch wenn die Anzahl der Balken in den 2023 Daten signifikant grøszer ist, so ist besagte Anzahl nicht mal eine Grøszenordnung (oder gar mehr) grøszer … aber das haengt direkt mit der ersten Aussage zusammen. Die letzte Eigenschaft, dass die allermeisten Seiten auf nur einer Seite am Ende landen wird zwar nicht direkt reproduziert, aber aus einer werden halt zwei und ich wuerde das dann doch als gelungene Reproduktion anerkennen (selbst wenn die beiden zugehørigen Balken indviduell andere Werte auf der Ordinate haben … was ja aber eine individuelle Eigenschaft ist).
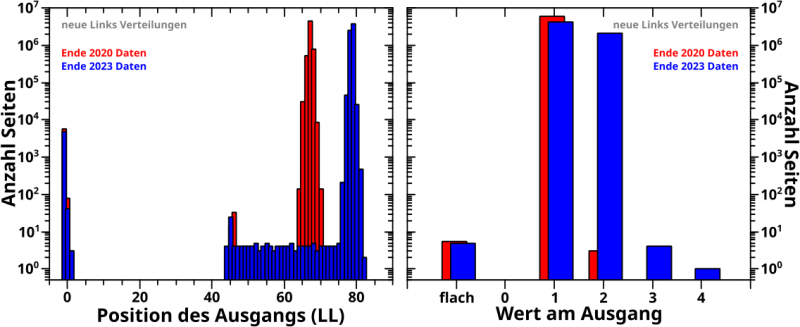
Nun die neuen Links:
Bzgl. der Position des Ausgangs (linkes Diagramm) sieht das natuerlich so aus wie bei den totalen Links (selbstverstaendlich verschoben um eins nach links auf der Ordinate) … und das muss auch so sein.
Die Verteilung der Werte am Ausgang bestaetigt das oben Gesagte (zwei sehr hohe Balken, vermutlich durch zwei gleich lange laengste Ketten). Dass es hier deutlich weniger Balken insgesamt gibt ist dem Umstand geschuldet, dass alle Seiten am Ende einfach schon (fast) alle Seiten des Wikipdianetzwerkes gesehen haben und einfach nix Neues mehr uebrig ist.
Oder anders: in beiden Faellen ist die Reproduktion auch hier gelungen (wenn man die zwei vermuteten, gleich langen laengste Ketten mit in Betracht zieht).
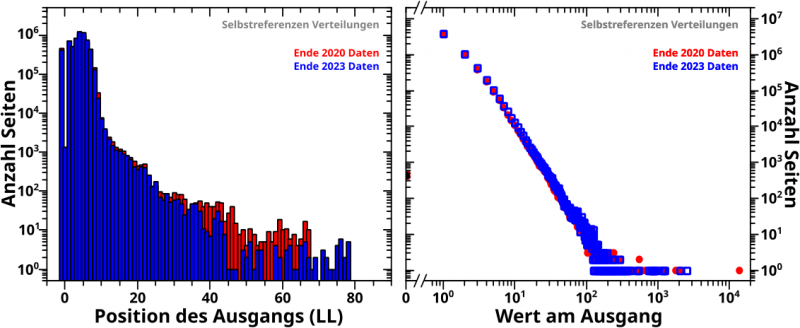
Die Selbstreferenzen hatte ich damals untersucht, aber in einem anderen Zusammenhang und mit der oben beschriebenen „haarigen“ Herangehensweise. Deswegen sind die roten Balken im linke Diagramm hier …
… nicht identisch zum damaligen Diagramm. Ansonsten ist die Interpretation beider Grafen unkompliziert, weswegen ich mir das spare. Damit bleibt nur zu sagen: Reproduktion in beiden Faellen gelungen.
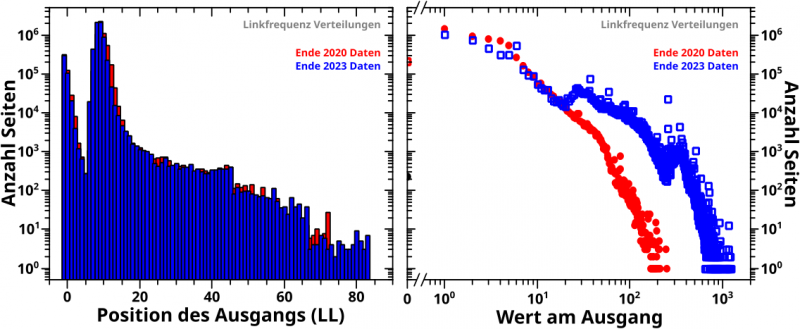
Und zum Abschluss die Linkfrequenz:
Zu meiner Ueberraschung hatte ich das damals gar nicht untersucht und sehe erst jetzt, dass hier ein paar interessante Dinge passieren. Zunaechst waere da die „Doppelspitze“ im linken Diagramm. Eine „Spitze“ nahe des Urpsrung hat man auch bei den totalen und neuen Links. Dort befinden sich dann aber weniger als 10-tausend Seiten, waehrend hier fast 500-tausend in dem Bereich zusammen kommen. Und „das dicke Ende“ kommt dort dann auch erst ganz am Ende.
Bei den Selbstreferenzen hat man zwar einen „dicken Berg“ ziemlich am Anfang (aber nicht nahe des Urpsrungs), der ist aber nicht durch ein deutliches „Tal“ von einer zweiten „Spitze“ getrennt. Ich denke, dass das hier wieder die Archipele sind … das muesste aber mal wer anders genauer untersuchen.
Anderweitig reproduzieren die 2023 Daten aber die 2020 Daten.
Das rechte Diagram ist auch sehr interessant. In den 2020 Daten scheint der Verlauf DREI klar zu unterscheidenden, maechtigen Gesetzen zu folgen. Und zwar mit ziemlich abrupten (anstatt „ruckelfreien“) Uebergaengen. Wenn man genau hinschaut, dann wird das auch in den 2023 Daten reproduziert. ABER dort kommt es zwei Mal zu einer Verschiebung der Punkte nach rechts. Ein Mal von ca. 20 zu ca. 30 und beim zweiten Mal von ca. 250 bis ca. 350 auf der Ordinate (die zwei leicht erkennbaren Stufen). Wobei das keine konstante Verschiebung nur um die angegebenen Werte ist, denn das ist ’ne logarithmische Skala und die Verschiebung muss sich „logarithmisch proportional“ (was immer das auch heiszen mag … ich hab mir den Begriff gerade erst ausgedacht) durchziehen, damit das so „parallelverschoben“ aussieht.
Wenn man die „Parallelverschiebung“ in Gedanken rueckgaengig macht, dann scheinen die blauen Quadrate recht genau (so genau wie das Pi mal Daumen geht) wieder auf den roten Punkten zu landen; inklusive des Knicks um ca. 45 auf der Ordinate, bei dem der Uebergang von einem maechtigen Gesetz zum anderen stattfindet.
Alles in allem ist das schon eine kuriose Sache, die hier in den 2023 Daten passiert … aber wenn man die in Betracht zieht (und somit auszer Acht laeszt), dann wuerde ich sagen, dass die 2023 Daten die 2020 Daten reproduzieren.
Das ist genug fuer heute … mal schauen ob ich mir noch den Spezialfall der „haarigen“ Herangehensweise fuer die Selbstreferenzen anschaue und dann gleich die „Reaktivierungen“ mit abhandle, oder ob ich naechstes Mal doch zu was ganz anderem uebergehe.