Beim letzten Mal schrieb ich:
Das muesste man sich mal in kumulativer Darstellung anschauen […].
mit dem expliziten Hinweis:
[…] mach ich aber nicht mehr.
Natuerlich hat mir das keine Ruhe gelassen und ich hab das jetzt doch noch gemacht.
Das Gute ist, dass ich dadurch fix noch zwei Analysewerkzeuge geschrieben gehackt habe, die ich sowieso øfter mal brauche und das ist gut, dass die jetzt mal systemati- und generalisiert (ich bin mir ziemlich sicher, dass man das so nicht machen kann … ich lass das dennoch einfach mal so stehen) sind.
Weil ich heute weder beschreiben muss, was man hier …
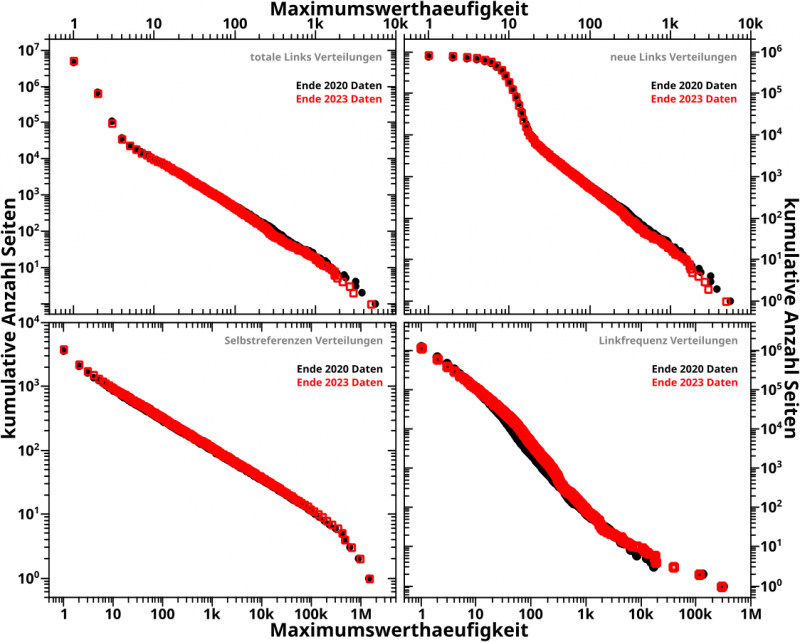
… sieht (denn das ist das Gleiche wie beim letzen Mal … mglw. sogar das Selbe, aber da bin ich mir nicht ganz so sicher, denn es sieht ja anders aus), noch was kumulative, doppellogarithmische Diagramme sind und warum man das so machen will (wenn ihr, meine lieben Leserinnen und Leser das nicht mehr wisst, muesst ihr nur dem Link im ersten Zitat folgen), muss ich fast gar nix dazu schreiben.
Nur zwei Sachen seien gesagt. Zum Einen habe ich mich jetzt doch an die kumulative Darstellung gemacht, um zu schauen ob die Punkte im langen Schwanz des urspruenglichen Histogramms zu den Selbstreferenzen dem maechtigen Gesetz folgen, welches man aus den Daten zwischen Maximumswerthaeufigkeiten von 1 und 100 (im urpsruenglichen Histogramm) erwartet. Im Diagramm links unten sieht man wieder einmal, wie krass kumulative log-log-Darstellungen sind, denn das besagte maechtige Gesetz kann man nun ueber FUENF (!) zusaetzliche (!) Grøszenordnungen als gegeben annehmen.
Zum Zweiten reproduzieren die 2023 Daten wieder die 2020 Daten. Aber das war zu erwarten, denn die Diagramme hier benutzen schlieszlich die selbe Datengrundlage.
Naechstes mal dann … was anderes.
Leave a Reply