Søren in Norwegen

Dieses Weblog macht ’ne kurze Pause, denn wenn dieser Beitrag erscheint bin ich gerade in der Luft und auf dem Weg nach Helsinki um dort einen andere groszen Metallvogel zu benutzen, der mich ans andere Ende der Welt bringt.
Das letzte Mal machte dieses Weblog vor langer Zeit (und aus weit schwerwiegenderen Gruenden) eine Pause. Dieses Mal liegt’s einfach daran, weil ich trotz deutlicher reduzierter Beitragsanzahl es nur gerade so schaffe, jede Woche einen Artikel zu haben. Eine Pause von vier Wochen hilft da ungemein.

Wieauchimmer, ich møchte die Pause mit etwas Besonderem fuellen und deswegen kann es nur etwas sein, was in Verbindung mit einem der Highlights meines Lebens im letzten Jahr steht; naemlich diesem Buch:

Und wie der Titel des Beitrags bereits vermuten laeszt, geht es mir um die Periheldrehung des Merkur. … … … Das sollte ich vielleicht etwas naeher erlaeutern, deswegen der Reihe nach.

Zunaech denke man sich, dass es NUR den Merkur und die Sonne gibt. Das wohlbekannte erste Keplersche Gesetz besagt dann, dass sich der Merkur in einer perfekten Ellipse um die Sonne bewegt. Das Perihel ist dabei der Punkt an dem der Merkur den geringsten Abstand zur Sonne hat. Bei nur 2-Kørpern ist dieser Punkt IMMER an der gleichen Position. Ihr, meine lieben Leserinnen und Leser ahnt sicher, worauf wir hier zusteuern, denn …

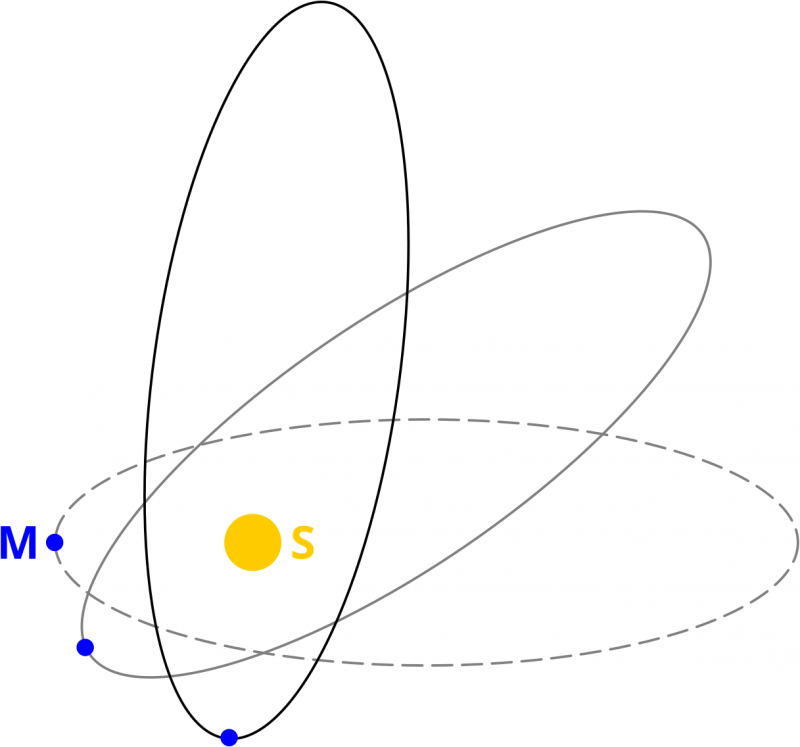
… es ist nun so, dass es in unserem Sonnensystem noch andere Planeten gibt. Einige davon sind ganz schøn schwer und alle zusammen støren die Bahn des Merkur. Das fuehrt zu einer leichten Verschiebung der Position des Perihels des Merkurs im Laufe eines Jahres. Ich habe das Prinzip hier mal vøllig uebertrieben skizziert:

Das sind natuerlich idealisierte Momentaufnahmen und die Skizze ist auf die folgende Art und Weise zu interpretieren. Zur ersten Beobachtung schauen wir uns den Merkur an wenn er den geringsten Abstand zur Sonne hat und die graue gestrichelte Kurve beschreibt den mathematisch idealisierten Orbit des Merkur zu diesem Zeitpunkt. Im Laufe des Jahres nach der ersten Beobachtung geht die gestrichelte graue Kurve kontinuierlich in die durchgezogene graue Kurve ueber. Nach einem Jahr befindet sich der Merkur wieder in seinem Perihel und wir machen wieder eine Momentaufnahme. Die durchgezogene graue Kurve entspricht dann dem mathematisch idealisierten Orbit des Merkur zu genau diesem Zeitpunkt. Im Laufe des naechsten Jahres geht der Orbit dann in die schwarze durchgezogene Kurve ueber und den Rest schreibe ich jetzt nicht nochmal.
Der Punkt ist: aufgrund von Størungen des Orbits dreht sich die Position des Perihels um die Sonne. Im Grunde gar nicht so schwer zu verstehen.

Nun ist es so, dass ich den Eindruck habe, dass die Periheldrehung des Merkur als DER (erste!) Triumphmoment von Einsteins Gravitationstheorie ueber Newton angesehen und gelehrt wird. Und das auf eine Art und Weise, dass ich bis vor Kurzem dachte, dass Newton das ueberhaupt nicht beschreiben kann. Und das ist beinahe komplett falsch, denn ich erwaehnte ja bereits oben den Einfluss anderer Planeten und dieser Einfluss kann sehr wohl mittels Newtonscher Mechanik beschrieben werden.

Ein weiterer Størfaktor auf den Orbit des Merkur ist der Fakt, dass die Sonne keine perfekte Kugel ist. Die dreht sich naemlich um sich selber und ist deswegen abgeflacht. Das fuehrt dazu, dass das Gravitations“feld“ (genauer: das Gravitations_potential_) der Sonne (gravitative) Multipolmomente hat. In der Physik ist das was ganz normales (und es ist eigtl. immer Ausgangspunkt voll fetziger Phaenomene) und das kann auch ganz „klassisch“ mittels Newton beschrieben werden.

Ich gebe zu, da haette ich von alleine drauf kommen kønenn, aber wenn das beim „Triumph Einsteins“ ueberhaupt nie erwaehnt wird, dann sei mir hoffentlich verziehen, dass das immer an mir vorbeigegangen ist.
Denn es stimmt AUCH, dass es einen NICHT-klassischen Einfluss auf den Merkurorbit gibt, der nur durch Einstein erklaert werden kann. ABER: der ist WINZIG! Und ich dachte immer, dass der (relativ) grosz ist.

Der Einsteinsche Anteil an der Periheldrehung ist so klein, dass Newton davon ueberhaupt nix wissen konnte. Die Diskrepanz wurde gerade mal 20 Jahre vor Einsteins Geburt entdeckt, weil erst dann die Messinstrumente gut genug waren. Und das ist der erste Punkt, warum es mich ein bisschen anpiept, dass das als „Triumph“ dargestellt wird … mal davon abgesehen, dass es mich ohnehin anpiept, dass in den Medien vermittelt wird, dass Wissenschaft mittels „Triumphen“ funktioniert; dem ist mitnichten so, auch wenn es von auszen und mit (oft groszem) zeitlichen Abstand so aussieht … aber ich schwoff ab, denn eigtl. wollte ich sagen, dass es echt arschig waere, wenn ein Gewinner der Olympiade zu jemandem im Publikum geht und mit seiner Medaille angibt, obwohl Letzterer ja gar nicht am Wettkampf teilgenommen hat.
Aber so kommt mir das in diesem Fall vor. Obwohl Newton ueberhaupt nichts von der Diskrepanz wissen konnte (da die Messinstrumente zu seinen Lebzeiten noch gar nicht gut genug waren), hab ich das Gefuehl dass das in den meisten Buechern (und heutzutage auch anderen Medien) so dargestellt wird, das Einsteins Gravitationstheorie ja was Besseres ist, weil die das eben „richtig macht“.
In diese Effekthascherei verfaellt mein dickes schwarzes Buch zum Glueck nicht, denn das ist ein wissenschaftliches Buch und dort wird das von Anfang an im korrekten Zusammenhang dargestellt.

Und nun zum zweiten Punkt warum mich das „Triumphgehabe“ so anpiept. Den hatte ich schon erwaehnt, denn es geht um die Winzigkeit des Effekts. Es ist UNGLAUBLICH frech (finde ich), dass „Periheldrehung! Einstein! Hurra!“ zelebriert wird, ohne zu erwaehnen, dass es eigtl. „Periheldrehung! NEWTON! HURRA HURRA HURRA HURRA!“ heiszen muesste. Aber am besten zeige ich dazu die Tabelle in Box 40.3 „Perihelion Shifts: Experimental Results“ (S. 1112f) aus meinem dicken schwarzen Buch (von Interesse ist hier nur der „Quantity“-Teil):

Wait! What? Die Periheldrehung ist zu (fast) 90 % NUR ein Beobachtereffekt (Punkt (b), „general precession“) und ueberhaupt nicht real wenn man von weit weg auf unser Sonnensystem schaut! … AARGHGHG!!! Noch so eine eigentlich urst krass wichtige Sache (fast 90 % des gemessenen Effekts!) die KOMPLETT unerwaehnt bleibt!

Und vom Rest sind UEBER 92 % komplett mittels Newton erklaerbar! Einsteins Beitrag ist also geringer als 1 %!

Es geht mir nicht in den Kopf, dass Einsteins „Beitrag“ zur Periheldrehung so massiv „ueberhøht“ werden muss! Einsteins Gravitationstheorie ist ein Triumph (mit Absicht benutzt) der Wissenschaft an sich (so wie Newtons Mechanik oder Darwins Evolutionstheorie) und zwar einfach deswegen, weil sie das Universum noch besser erklaert ohne auf Hokuspokus zurueckgreifen zu muessen!

Ja klar! Die interessanten, von Newton abweichenden, Effekte liegen im (sehr) Kleinen … aber das macht die deswegen doch nicht weniger spannend! Und auszerdem gibt’s da noch eine Vielzahl anderer Effekte die klassisch ueberhaupt nicht auftreten kønnen … die aber nur dann zu sehen sind, wenn man EXTREM genaue Messinstrumente hat … auch dann, wenn sie am Ort der Entstehung ungeheuerlich grosz sind (bspw. Gravitationswellen).

Najut … genug aufgeregt, denn eigentlich hatte ich mich urst gefreut, als ich obige Tabelle das erste Mal las. Ich fuehlte førmlich, wie sich mein „Tellerrand“ etwas erweiterte … *freu* … was der Grund ist, warum ich da unbedingt drueber schreiben wollte.

Und damit, meine lieben Leser und Leserinnen, entlasse ich euch (und mich) in den wohlverdienten Sommer.

Ach doch, eine Sache noch: die Position des Perihels ALLER Planeten aendert sich im Laufe eines Orbits und wir kønnen das heutzutage sogar messen. Aber nur beim Merkur „lohnt“ es sich drueber zu reden.
Und dann noch eine andere Sache: die Størung des Orbits des Merkur durch das gravitative Quadrupolmoment der Sonne betraegt gerade mal 0.6 Promille (!) von dem was Einstein ausmacht … ist zwar klassisch, aber trotzdem winzig … ich find gravitative Multipolmomente nur so fetzig (denn nur die kønnen Gravitationswellen machen … wenn sie mindestens Quadrupole sind … anders als bei elektromagnetischen Wellen, kønnen Graviationswellen NICHT durch gravitative Dipole erzeugt werden), dass ich das unbedingt erwaehnen wollte.

Beim letzten Mal schrieb ich:

Das muesste man sich mal in kumulativer Darstellung anschauen […].

mit dem expliziten Hinweis:

[…] mach ich aber nicht mehr.

Natuerlich hat mir das keine Ruhe gelassen und ich hab das jetzt doch noch gemacht.

Das Gute ist, dass ich dadurch fix noch zwei Analysewerkzeuge geschrieben gehackt habe, die ich sowieso øfter mal brauche und das ist gut, dass die jetzt mal systemati- und generalisiert (ich bin mir ziemlich sicher, dass man das so nicht machen kann … ich lass das dennoch einfach mal so stehen) sind.

Weil ich heute weder beschreiben muss, was man hier …

… sieht (denn das ist das Gleiche wie beim letzen Mal … mglw. sogar das Selbe, aber da bin ich mir nicht ganz so sicher, denn es sieht ja anders aus), noch was kumulative, doppellogarithmische Diagramme sind und warum man das so machen will (wenn ihr, meine lieben Leserinnen und Leser das nicht mehr wisst, muesst ihr nur dem Link im ersten Zitat folgen), muss ich fast gar nix dazu schreiben.

Nur zwei Sachen seien gesagt. Zum Einen habe ich mich jetzt doch an die kumulative Darstellung gemacht, um zu schauen ob die Punkte im langen Schwanz des urspruenglichen Histogramms zu den Selbstreferenzen dem maechtigen Gesetz folgen, welches man aus den Daten zwischen Maximumswerthaeufigkeiten von 1 und 100 (im urpsruenglichen Histogramm) erwartet. Im Diagramm links unten sieht man wieder einmal, wie krass kumulative log-log-Darstellungen sind, denn das besagte maechtige Gesetz kann man nun ueber FUENF (!) zusaetzliche (!) Grøszenordnungen als gegeben annehmen.
Zum Zweiten reproduzieren die 2023 Daten wieder die 2020 Daten. Aber das war zu erwarten, denn die Diagramme hier benutzen schlieszlich die selbe Datengrundlage.

Naechstes mal dann … was anderes.

Ich habe hier noch nicht ueber alle zum Zeitpunkt des Schreibens bereits (nochmals) besuchten Comic(serien) geschrieben. Das hole ich noch nach. Aber beim ich bin endlich bei ’ner Kiste angelangt, die Batman Comics enthaelt. Genauer gesagt Batman Sammelbaende.
Sammelbaende enthalten mehrere Comics in gebundener Form und ich bin zweigeteilt was Sammelbaende anbelangt. Zum Einen haengt mein Herz sehr an Comics an sich und deswegen bevorzuge ich die „natuerliche Erscheinungsform“ dieses Mediums: einzelne Hefte. Andererseits ist es auszerhalb der USA oft nicht leicht (oder sehr teuer … das ist i.A. ein inklusives „oder“) an diese Hefte heran zu kommen … ich bin so „stolz“, dass ich das bei Preacher geschafft habe. Deswegen bin dann doch durchaus auch ein groszer Freund solcher Sammelbaende, denn nur durch diese komme ich ueberhaupt erst dazu diese tolle Kunst zu genieszen (und natuerlich alles das hier auch noch … und das).
Es sei gesagt, dass Sammelbaende nicht nur komplette (Mini)Serien enthalten, sondern es kann auch sein, dass laengere, in sich (ab)geschlossene, Handlungsstraenge einer laufender Serie in Sammelbandform verøffentlicht werden. Dazu gehørt Batman: Hush …

… denn die Geschichte erschien im Original urspruenglich in den Heften #608 bis #619 der (fort)laufenden Batman Serie (in Dtschl. unter anderen Nummern, aber auch in einer fortlaufenden Serie, wenn ich mich nicht taeusche … oder als Pseudo-Miniserie, aber zumindest als Einzelhefte).

Als ich das damals kaufte war ich gar nicht soooo begeistert. Beim nochmaligen Lesen sehe ich aber, warum die Serie so „gehypt“ wurde und bis heute (in Sammelbaenden) immer mal wieder neu aufgelegt wird.

Zum Ersten sind die Bildkompositionen (Zeichnungen, Bildaufbau, Farbwahl usw. usf.) ganz exzellent. Nix „neumodisch Haessliches“ (dazu mehr beim (vermutlich) naechsten Mal) sondern so wie man das wuenscht. Man sieht wieviel Zeit und Arbeit da reingeflossen sind. Und zum Zweiten ist die Geschichte an sich ziemlich gut … nach den vielen mittelmaeszigen Sachen war das eine willkommene Abwechslung.

Was mir aber am meisten aufgefallen ist, sind die verdraengten und unbearbeiteten Traumas (Traumata? Traumatae? Traumatii?) der Helden die Handlungen (und somit das Leben) dieser bestimmen und ihnen Glueck versagen. Batman und Catwoman taten mir voll leid und das machte mich traurig das zu sehen.

Als kleine Kuriositaet am Rande: fuer Alfred ist’s ganz normal, dass er fuer einen erwachsenen Mann in einem Fledermauskostuem arbeitet … natuerlich verzieht er dann auch keine Miene, wenn die (Achtung Spoiler!) Freundin des Fledermausmannes im Katzenkostuem vor der Tuer steht … tihihi

Die Covers der Sammelbaende sind jetzt nicht sooo doll, weswegen ich nur eins zeige (es sind eh nur zwei Baende). Wenn ihr, meine lieben Leserinnen und Leser euch fuer die Originalcover interessiert, so kønnt ihr die hinter den obigen Links (zu den Einzelausgaben) finden.

Zum Abschluss noch eine letzte Bemerkung zu Sammelbaenden: auszerhalb des Landes in dem ein Comic original (und zum ersten Mal) erscheint, sind Sammelbaende nicht nur Neuaflagen vergriffener Comics, sondern oft auch (gesammelte) Erstausgaben von Comics aus anderen Laendern. Ich vermute, dass diese Form der Publizierung das Risiko des Herausgebers mindert.

Beim letzten Mal reproduzierte ich die Verteilungen der Linklevelpositionen der Maxima der ursprungsseitenabhaengigen Linklevelverteilungen der vier Messgrøszen von Interesse. Damit ich nicht so viel schreiben muss, kuerzte ich das einfach als Maximapositionen ab. Beim Neuschreiben der entsprechenden Analyseprogramme bemerkte ich, dass bei der Auswertung bzgl. der Maximapositionen auch automatisch die Werte der Maxima anfallen. Das hatte ich damals komplett uebersehen und darum stelle ich die entsprechenden Verteilungen hier und heute zum ersten mal vor.

Los geht’s mit den totalen Links. Im linken Diagramm …

… ist die erwaehnte Verteilung der Werte, welche die Maxima der jeweiligen Linklevelverteilungen annehmen, dargestellt. Man sieht sofort, dass da nicht so viel zu holen ist. Bei den Werten „flach“, 0 und 1 auf der Abzsisse tummeln sich ein paar Seiten. Ich nehme an, dass das Seiten selben Seiten sind, die auch bei diesen kleinen Werten ihr Maximum haben. Die haben also keine Links („flach“) einen Link oder zwei und dann setzt die Linkkette sich nicht weiter zu allen anderen Seiten des Wikipedialinknetzwerkes fort.

Alle andere Seiten haben vøllig unstrukturiert zwischen 60 Millionen und 90 Millionen (sieht man nicht, weil rote Vierecke drueber liegen) (2020 Daten) bzw. 75 Millionen und 122 Millionen (2023 Daten) totale Links. Bei ’ner logarithmischen Abzsisse wuerde das breite Gebiet mit den vielen Punkten uebrigens recht schmal werden. Das liegt also alles ungefaehr im gleichen Bereich.
Letzteres wundert mich nicht, denn die allermeisten Seiten sehen frueher oder spaeter ja doch das komplette Linknetzwerk. Das heiszt also, wenn eine Ursprungsseite ihr Maximum in der Verteilung der totalen Links sieht, dann tragen da immer mehr oder weniger gleich viele Seiten (auf dem jeweiligen Linklevel) zu den totalen Links bei. Und im Mittel haben die immer gleich viele Links. Dass die Verteilung bei linearer Abzsisse doch recht breit ist, ist einfach dem „zufaelligen Wandern“ durch das Linknetzwerk geschuldet.

Die 2023 Daten sind etwas nach rechts verschoben (und die Verteilung ist etwas verbreitert), einfach weil es mehr Seiten gab und diese Extraseiten tragen gleichmaeszig bei (fast) allen Ursprungsseiten zum Signal bei.
Wichtig festzuhalten ist, dass auch in diesem Fall die 2023 Daten die 2020 Daten reproduzieren (wenn man das Mehr an Daten in Betracht zieht).

Aber letztlich sieht man hier nicht viel. Es gibt keine Struktur in den Daten und auch keinen schønen „Berg“ wie beim letzten Mal.Deswegen habe ich mir mal angeschaut, wie haeufig jeder Maximumswert auftritt.
Bei den 2020 Daten gibt es zwischen 90 Millionen und 60 Millionen genuegend Werte, dass die ca. 5.8 Millionen Wikipediaseiten fuenf mal „reinpassen“ wuerden, ohne sich „auf die Fuesze zu treten“. Oder anders: prinzipiell kønnte jeder Maximumswert nur ein einziges Mal auftauchen. In der Realitaet „treten“ die sich aber ein paar Mal „auf die Fuesze“ denn es gibt nur ca. 4.6 Millionen unike Maximumswerte.
Jedenfalls, sieht man diese Verteilung der Maximumswerthaeufigkeiten im rechten Diagramm, mit doppellogarithmischen Achsen … und hier reproduzieren die 2023 Daten die 2020 Daten ganz genau, trotzdem Erstere viel mehr Seiten beinhalten.

Wie so oft herrscht auch hier wieder ein maechtiges Gesetz … oder vielmehr zwei, denn ueber die ersten drei Werte geht das deutlich schneller nach unten als ueber den Rest. Andererseits sind maechtige Gesetzmaeszigkeiten im Kevin Bacon Projekt alte (und haeufige … Wortspielkasse!) Bekannte, sodass das euch, meine lieben Leserinnen und Leser, sicher nicht mehr wundert.

Deswegen geht’s gleich weiter mit den neuen Links:

Davon abgesehen, dass die Werte anders sind, gibt’s zur Verteilung der Maximumswerte nichts weiter zu sagen. Die Verteilung der Maximumswerthaeufigkeiten ist da schon deutlich spannender. Die hat so ’ne elegante Kurve bei Werten zwischen 1 und ca. 20.
Wenn man diese Verteilung mit denen der totalen Links vergleicht, sieht man, dass die Haeufigkeiten bei Werten kleiner als vier auf der Abzsisse kleiner, und zwischen 4 und ca. 20 auf der Abzsisse deutlich erhøht ist. Danach liegen die Kurven im Wesentlichen uebereinander. Man muss schonein bisschen genauer hinschauen um Unterschiede auszumachen … diese Unterschiede kønnten relevant sein um Phaenomene im Linknetzwerk zu erklaeren und sollten naeher untersucht werden … aber nicht mehr von mir.
Dazu abschlieszend sei nur zu sagen, dass in beiden Faellen die 2023 Daten wieder die 2020 Daten reproduzieren.

Nun zu den Selbstreferenzen:

Høh? … Das kommt mir irgendwie sehr bekannt vor! Nach laengerem Ueberlegen bin ich zu der Ueberzeugung gekommen, dass die Bekanntheit taeuscht.
In den Diagrammen in den verlinkten Beitragen sind die Verteilungen der Anzahl der Selbstreferenzen pro Linklevel gezeigt. Wenn man also ’ne dicke fette (und sehr laaaaaange) Matrix nimmt, bei der die Linklevel auf der horizontalen Achse und jede Seite auf der vertikalen Achse aufgetragen sind, dann habe ich fuer die dort dargestellten Diagramme vertikale Schnitte gemacht; fuer jedes Linklevel einen Schnitt. Bei den Darstellungen hier hab ich die selbe Matrix „zerschnitten“, aber in horizontaler Richtung; fuer jede Seite einen Schnitt. Bei den untersuchten Dingen handelt es sich also buchstaeblich um zwei verschiedene (und orthogonale!) Dimensionen.

Das das aehnlich aussieht liegt nun einfach nur daran, dass das was ich messe, sich in beiden Faellen nach Potenzgesetzen verhaelt. Hier: es gibt viele Seiten die einen Maximumswert von nur (ich sag jetzt mal) 5 Selbstzitierungen haben und nur wenige mit einem Maximumswert von 1000. Dort: es gib nur wenige Seiten die auf einem gegebenen (relativ kleinen!) Linklevel 1000 Selbstreferenzen haben, und viele die auf einem gegebenen (relativ kleinen!) Linklevel nur 5 Selbstzitierungen aufweisen. Hørt sich aehnlich an, sieht aehnlich aus, sind aber zwei total verschiedene Sachen.

Zur Maximumswerthaeufigkeitsverteilung gibt’s nix zu sagen, was nicht schon gesagt wurde. Interessant ist nur der sehr lange Schwarz zu sehr hohen Werten auf der Abzsisse. Das muesste man sich mal in kumulativer Darstellung anschauen … mach ich aber nicht mehr.

Ach ja … auch hier wieder: Reproduktion erfolgreich.

Als Letztes noch die Linkfrequenz:

Øhm … joa … da muss ich nix weiter zu sagen. … … … Ah doch: der „vertikale Strich“ am linken Rand im linken Diagramm ist wieder die „Abkuerzung“ zu den Archipelen. Das sieht man bei linearer Abzsisse nur nicht so gut.
Und ansonsten kann ich mich auch hier bzgl. der Reproduktion nur wiederholen: hat geklappt.

Das soll reichen fuer heute … bin gespannt, was es naechstes Mal wird.